
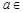 R,函数
R,函数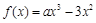 .
.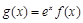 在区间[0,2]上是减函数,求实数a的取值范围.
在区间[0,2]上是减函数,求实数a的取值范围. ;(2)
;(2) .
. 求解即可;(2)求导数,利用
求解即可;(2)求导数,利用 在
在 上是减函数的充要条件是
上是减函数的充要条件是 在
在 上恒成立.规律总结:利用导数研究函数的性质是常见题型,主要是通过导数研究函数的单调性、求单调区间、求极值、最值以及不等式恒成立等问题,往往计算量较大,思维量大,要求学生有较高的逻辑推理能力.
上恒成立.规律总结:利用导数研究函数的性质是常见题型,主要是通过导数研究函数的单调性、求单调区间、求极值、最值以及不等式恒成立等问题,往往计算量较大,思维量大,要求学生有较高的逻辑推理能力.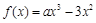 ,得
,得 ,
, ,解得
,解得 ,
, .
. ,得
,得 ,
,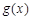 在区间[0,2]上是减函数,
在区间[0,2]上是减函数, 在区间[0,2]上恒成立,
在区间[0,2]上恒成立, 在区间(0,2]上恒成立即可,
在区间(0,2]上恒成立即可, ,只需要
,只需要 在(0,2]上恒成立,
在(0,2]上恒成立, ,则
,则 恒成立,
恒成立, 在区间(0,2]上单调递减,
在区间(0,2]上单调递减, 的最小值
的最小值 ,故
,故 ,
, .
.

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源:不详 题型:解答题
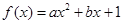 (
(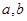 为实数,
为实数,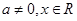 ),
),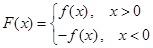 ,⑴若
,⑴若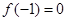 ,且函数
,且函数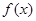 的值域为
的值域为 ,求
,求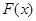 的表达式;
的表达式;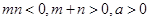 ,且函数
,且函数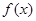 为偶函数,判断
为偶函数,判断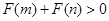 是否大0?
是否大0?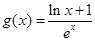 ,当
,当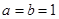 时,证明:对任意实数
时,证明:对任意实数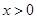 ,
,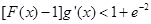 (其中
(其中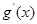 是
是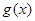 的导函数) .
的导函数) .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 时,每小时消耗的煤价值
时,每小时消耗的煤价值 元,至于其他费用每小时要
元,至于其他费用每小时要 元,问火车行驶的速度为多少时,才能使火车从甲城开往乙城的总费用最省?
元,问火车行驶的速度为多少时,才能使火车从甲城开往乙城的总费用最省?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ;③(ex)′=ex;④(
;③(ex)′=ex;④( )′=x;⑤(x·ex)′=ex+1.
)′=x;⑤(x·ex)′=ex+1.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com