
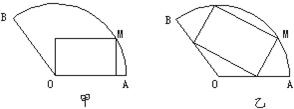
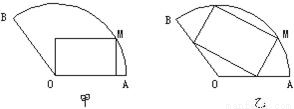
 将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.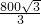 [cos(2α-60°)-cos60°].
[cos(2α-60°)-cos60°].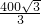 cm2.
cm2.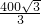 >200,
>200,

科目:高中数学 来源: 题型:
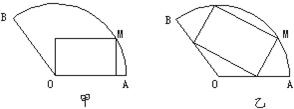 将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.查看答案和解析>>
科目:高中数学 来源: 题型:044
将一块圆心角为
120°,半径为20cm的扇形铁片裁成一块矩形,如图所示,有两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,试问哪种裁法能得到矩形的面积最大,并求出这个最大值.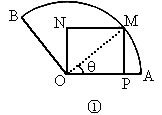
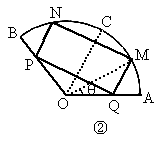
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市首师大附中高一(下)期中数学试卷(解析版) 题型:解答题
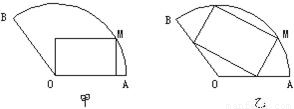
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:4.3 两角和与差、二倍角的公式2(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com