考点:有理数指数幂的化简求值,基本不等式在最值问题中的应用
专题:计算题,三角函数的图像与性质
分析:令a=3
x,b=3
y,则a>0,b>0,由3
x+3
y=9
x+9
y,得a+b=a
2+b
2,即有
(a-)2+(b-)2=,
令a-
=
cosθ,b-
=
sinθ,θ∈(-
,
),有
=
+
(sinθ+cosθ)-
sinθcosθ,
令sinθ+cosθ=t,则sinθcosθ=
,有t=
sin(θ+
),可求t∈(0,
],从而可得
+
(sinθ+cosθ)-
sinθcosθ=
-
(t-
)
2,即可求
的取值范围.
解答:
解:令a=3
x,b=3
y,则a>0,b>0
∵3
x+3
y=9
x+9
y,∴a+b=a
2+b
2∴
(a-)2+(b-)2=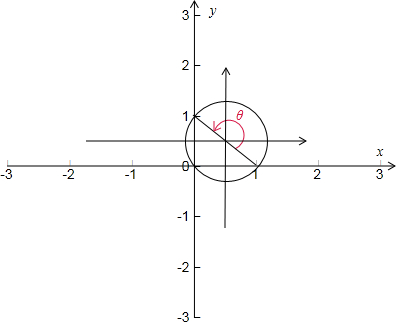
令a-
=
cosθ,b-
=
sinθ,θ∈(-
,
)
∴
=a
2+b
2-ab=a+b-ab=
+
cosθ+
+
sinθ-(
+
cosθ)(
+
sinθ)
=1+
cosθ+
sinθ-
-
cosθ-
sinθ-
sinθcosθ
=
+
(sinθ+cosθ)-
sinθcosθ
令sinθ+cosθ=t,则sinθcosθ=
有:t=
sin(θ+
)
∵θ∈(-
,
),∴θ+
∈(0,π),∴t∈(0,
]
∴
+
(sinθ+cosθ)-
sinθcosθ
=
+
t-
=1+
t-
t
2=1-
(t
2-
t+
()2)+
=
-
(t-
)
2∴当t=
时,取最大值
,当t趋向0时,最小值趋向1.
故
的取值范围是[1,
].
点评:本题主要考察了有理数指数幂的化简求值,基本不等式在最值问题中的应用,考察了转化思想,属于难题.




 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案