
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P
=1(a>b>0)的两个焦点分别为F1(-1,0),F2(1,0),且椭圆C经过点P![]() .
.
(1)求椭圆C的离心率;
(2)设过点A(0,2)的直线l与椭圆C交于M,N两点,点Q是线段MN上的点,且![]() =
=![]() +
+![]() ,求点Q的轨迹方程.
,求点Q的轨迹方程.
【答案】见解析
【解析】
解:(1)由椭圆定义知,
2a=|PF1|+|PF2|
=![]()
+![]() =2
=2![]() ,
,
所以a=![]() .
.
又由已知,得c =1,
所以椭圆C的离心率e=![]() =
=![]() =
=![]() .
.
(2)由(1)知,椭圆C的方程为![]() +y2=1.
+y2=1.
设点Q的坐标为(x,y).
①当直线l与x轴垂直时,直线l与椭圆C交于(0,1),(0,-1)两点,此时点Q的坐标为![]() .
.
②当直线l与x轴不垂直时,设直线l的方程为y=kx+2.
因为M,N在直线l上,可设点M,N的坐标分别为(x1,kx1+2),(x2,kx2+2),则|AM|2=(1+k2)x,|AN|2=(1+k2)x.
又|AQ|2=x2+(y-2)2=(1+k2)x2.
由![]() =
=![]() +
+![]() ,得
,得
![]() =
=![]() +
+![]() ,
,
即![]() =
=![]() +
+![]() =
=![]() .①
.①
将y=kx+2代入![]() +y2=1中,得
+y2=1中,得
(2k2+1)x2+8kx+6=0.②
由Δ=(8k)2-4×(2k2+1)×6>0,
得k2>![]() .
.
由②可知,x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
代入①中并化简,得x2=![]() .③
.③
因为点Q在直线y=kx+2上,所以k=![]() ,代入③中并化简,
,代入③中并化简,
得10(y-2)2-3x2=18.
由③及k2>![]() ,可知0<x2<
,可知0<x2<![]() ,
,
即x∈![]() ∪
∪![]() .
.
又点![]() 满足10(y-2)2-3x2=18,故x∈
满足10(y-2)2-3x2=18,故x∈![]() .
.
由题意知Q(x,y)在椭圆C内,
所以-1≤y≤1.
又由10(y-2)2=18+3x2有
(y-2)2∈![]() ,且-1≤y≤1,
,且-1≤y≤1,
则y∈![]() .
.
所以点Q的轨迹方程为10(y-2)2-3x2=18,
其中x∈![]() ,y∈
,y∈![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 的方程为
的方程为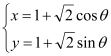 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)当![]() 时,判断直线
时,判断直线![]() 与
与![]() 的关系;
的关系;
(II)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
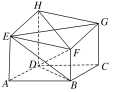
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线![]() 和直线
和直线![]() 交于点
交于点![]() .以
.以![]() 为起点,再从曲线
为起点,再从曲线![]() 上任取两个点分别为终点得到两个向量,记这两个向量的数量积为
上任取两个点分别为终点得到两个向量,记这两个向量的数量积为![]() .若
.若![]() 去九寨沟;若
去九寨沟;若![]() 去泰山;若
去泰山;若![]() 去长白山;
去长白山; ![]() 去武夷山.
去武夷山.
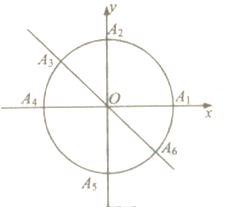
(1)若从![]() 这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
(2)按上述方案,小明在曲线![]() 上取点
上取点![]() 作为向量的终点,则小明决定去武夷山.点
作为向量的终点,则小明决定去武夷山.点![]() 在曲线
在曲线![]() 上运动,若点
上运动,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知M(x0,y0)是椭圆C:![]() +
+![]() =1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.
=1上的任一点,从原点O向圆M:(x-x0)2+(y-y0)2=2作两条切线,分别交椭圆于点P,Q.

(1)若直线OP,OQ的斜率存在,并记为k1,k2,求证:k1k2为定值;
(2)试问|OP|2+|OQ|2是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax+ln(x+1)(a∈R).
(1)当a=2时,求函数f(x)的极值点;
(2)若函数f(x)在区间(0,1)上恒有f′(x)>x,求实数a的取值范围;
(3)已知a<1,c1>0,且cn+1=f′(cn)(n=1,2,…),证明数列{cn}是单调递增数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,从a1,a2,a3,a4,a5,a6,a7中取走任意四项,则剩下三项构成等差数列的概率为( )
A. ![]() B.
B. ![]()
C.1或![]() D.1或
D.1或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com