
【题目】某乒乓球俱乐部派甲、乙、丙三名运动员参加某运动会的个人单打资格选拔赛,本次选拔赛只有出线和未出线两种情况.若一个运动员出线记![]() 分,未出线记
分,未出线记![]() 分.假设甲、乙、丙出线的概率分别为
分.假设甲、乙、丙出线的概率分别为![]() ,他们出线与未出线是相互独立的.
,他们出线与未出线是相互独立的.
(1)求在这次选拔赛中,这三名运动员至少有一名出线的概率;
(2)记在这次选拔赛中,甲、乙、丙三名运动员所得分之和为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(I)若曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,求
轴,求![]() 的值;
的值;
(II)求函数![]() 的极值;
的极值;
(III)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,求解下列问题(1)求函数f(x)的定义域;(2)求f(﹣1),f(12)的值;.
,求解下列问题(1)求函数f(x)的定义域;(2)求f(﹣1),f(12)的值;.
(1)求函数f(x)的定义域;
(2)求f(﹣1),f(12)的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,区间M=[a,b](a<b),集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有( )
,区间M=[a,b](a<b),集合N={y|y=f(x),x∈M},则使M=N成立的实数对(a,b)有( )
A.1个
B.2个
C.3个
D.无数多个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
(Ⅰ)若圆x2+y2=4在伸缩变换![]() (λ>0)的作用下变成一个焦点在x轴上,且离心率为
(λ>0)的作用下变成一个焦点在x轴上,且离心率为![]() 的椭圆,求λ的值;
的椭圆,求λ的值;
(Ⅱ)在极坐标系中,已知点A(2,0),点P在曲线C:ρ=![]() 上运动,求P、A两点间的距离的最小值.
上运动,求P、A两点间的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面关于集合的表示正确的个数是( )
①{2,3}≠{3,2}; ②{(x , y)|x+y=1}={y|x+y=1};
③{x|x>1}={y|y>1}; ④{x|x+y=1}={y|x+y=1}.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合A={x|x=m2﹣n2 , m∈Z,n∈Z},因为16=52﹣32 , 所以16∈A,研究下列问题:
(1)1,2,3,4,5,6六个数中,哪些属于A,哪些不属于A,为什么?
(2)讨论集合B={2,4,6,8,…,2n,…}中有哪些元素属于A,试给出一个普通的结论,不必证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l: 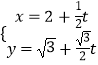 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(1)若点M的直角坐标为(2, ![]() ),直线l与曲线C交于A、B两点,求|MA|+|MB|的值;
),直线l与曲线C交于A、B两点,求|MA|+|MB|的值;
(2)设曲线C经过伸缩变换 ![]() 得到曲线C′,求曲线C′的内接矩形周长的最大值.
得到曲线C′,求曲线C′的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,△ABC是边长为2 ![]() 的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点.
的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点. 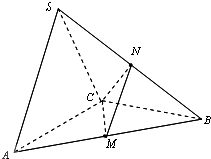
(1)证明:AC⊥SB;
(2)求三棱锥B﹣CMN的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com