
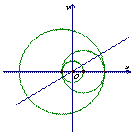
 设M1(0,0),M2(1,0),以M1为圆心,| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2),记作⊙M1;以M2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作⊙M2;……;以Mn为圆心,| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1),记作⊙Mn;……当n∈N*时,过原点作倾斜角为30°的直线与⊙Mn交于An,Bn.考察下列论断:
设M1(0,0),M2(1,0),以M1为圆心,| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2),记作⊙M1;以M2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作⊙M2;……;以Mn为圆心,| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1),记作⊙Mn;……当n∈N*时,过原点作倾斜角为30°的直线与⊙Mn交于An,Bn.考察下列论断:
当n=1时,![]() ;Ks当n=2时,
;Ks当n=2时,![]() ;当n=3时,
;当n=3时,![]() ;
;
当n=4时, ![]() ;当n=5时,
;当n=5时, ![]() ;……,
;……,
则推测一个一般的结论:对于n∈N*,![]() .
.
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
| m |
| x |
| m |
| 1+x |
| fn(0)-1 |
| fn(0)+2 |
| 4n2+n |
| 4n2+4n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•虹口区一模)已知圆O:x2+y2=4.
(2013•虹口区一模)已知圆O:x2+y2=4.| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:上海市奉贤区2011届高三12月调研测试数学理科试题 题型:044
设h(x)=![]() ,x∈[
,x∈[![]() ,5],其中m是不等于零的常数,
,5],其中m是不等于零的常数,
(1)写出h(4x)的定义域;
(2)求h(x)的单调递增区间;
(3)已知函数f(x)(x∈[a,b]),定义:f1(x)=min{f(t)|a≤t≤x}(x∈[a,b]),f2(x)=max{f(t)|a≤t≤x}(x∈[a,b]).其中,min{f(x)|x∈D}表示函数f(x)在D上的最小值,max{f(x)|x∈D}表示函数f(x)在D上的最大值.例如:f(x)=cosx,x∈[0,π],则f1(x)=cosx,x∈[0,π],f2(x)=1,x∈[0,π],当m=1时,设![]() ,不等式t≤M1(x)-M2(x)≤n恒成立,求t,n的取值范围;
,不等式t≤M1(x)-M2(x)≤n恒成立,求t,n的取值范围;
查看答案和解析>>
科目:高中数学 来源:2013年上海市虹口区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
 与圆O相交于A、B两点,求|AB|;
与圆O相交于A、B两点,求|AB|;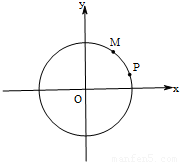
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com