Question

【题目】（本小题满分13分）

已知函数，（其中），其部分图像如图所示.

（I）求的解析式；

（II）求函数在区间上的最大值及相应的值。

Answer 1

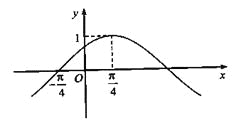
【答案】解：（I）由图可知，A="1 " ………………1分

………………2分

所以………………3分

又

所以………………5分

所以………………6分

（II）由（I）

所以

………………8分

………………9分

………………10分

因为

故：

当取得最大值………………13分

【解析】

分析：（1）先求出函数的周期，推出，利用图像所过的点，代入函数解析式，结合题中所给的范围，求得，从而得到的解析式；

（2）求出函数在区间上的最大值及相应的值.

详解：（1）由图可知，，，所以 ∴

又，且，所以-

所以．

（2）由（1）知，

所以=

因为，所以，．

故，当时，取得最大值．

分析：⑴先求周期，推出，利用,推出 ，得到的解析式；

⑵利用（1）求出函数的解析式，通过二倍角公式，确定角的范围，确定函数的最大值以及相应的x的值.