练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    实数x,y满足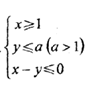，若函数z=x+y的最大值为4,则实数a的值为(     )

    A．2 B．3 C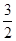． D．4

    A

    解析试题分析：由，得,则表示该组平行直线在轴的截距。又由约束条件作出可行域如图，先画出，经平移至经过和的交点时，取得最大值，代入，即，所以，故选.

    考点：线性规划求目标函数的最值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    已知实数满足不等式组则目标函数的最小值与最大值的积为()

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设变量满足，则的最大值和最小值分别为（    ）

    A．1，-1 B．2，-2 C．1，-2 D．2，-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知满足约束条件，则目标函数的最大值（   ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若原点和点分别在直线的两侧，则的取值范围是

    A． B． C．或 D．或

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知函数的图像如图所示，则的取值范围是（   ）

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设变量满足条件则点所在区域的面积为（  ）

    A．4B．6C．8D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知变量x,y满足约束条件，则z=x+2y的最小值为

    A．3 B．1 C．-5 D．-6

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    某旅行社租用A，B两种型号的客车安排900名客人旅行，A，B两种车辆的载客量分别为36人和60人，租金分别为1600元/辆和2400元/辆，旅行社要求租车总数不超过21辆，且B型车不能多于A型车7辆，则租金最少为(　　)

    A．31 200元 B．36 000元  C．36 800元  D．38 400元 

    查看答案和解析>>

    同步练习册答案