
【题目】如图,在三角形![]() 中,
中,![]() ,平面
,平面![]() 与半圆弧
与半圆弧![]() 所在的平面垂直,点
所在的平面垂直,点![]() 为半圆弧上异于
为半圆弧上异于![]() 的动点,
的动点,![]() 为
为![]() 的中点.
的中点.
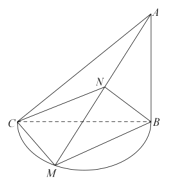
(1)求证:![]() ;
;
(2)求三棱锥![]() 体积的最大值.
体积的最大值.
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】某农场为了提高某品种水稻的产量,进行良种优选,在同一试验田中分两块种植了甲乙两种水稻.为了比较甲乙两种水稻的产量,现从甲乙两种水稻中各随机选取20株成熟水稻.根据每株水稻颗粒的重量(单位:克)绘制了如下茎叶图:
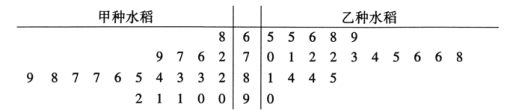
(1)根据茎叶图判断哪种水稻的产量更高?并说明理由;
(2)求40株水稻颗粒重量的中位数![]() ,并将重量超过
,并将重量超过![]() 和不超过
和不超过![]() 的水稻株数填入下面的列联表:
的水稻株数填入下面的列联表:
超过 | 不超过 | |
甲种水稻 | ||
乙种水稻 |
(3)根据(2)中的列联表,能否有![]() 的把握认为两种水稻的产量有差异?附:
的把握认为两种水稻的产量有差异?附: ;
;
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 由方程到
由方程到![]() 确定,对于函数
确定,对于函数![]() 给出下列命题:
给出下列命题:
①对任意![]()
![]() ,都有
,都有![]() 恒成立:
恒成立:
②![]()
![]() ,使得
,使得![]() 且
且![]() 同时成立;
同时成立;
③对于任意![]()
![]() 恒成立;
恒成立;
④对任意,![]()
![]()
![]() ,
,
都有![]() 恒成立.其中正确的命题共有( )
恒成立.其中正确的命题共有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冬季历来是交通事故多发期,面临着货运高危运行、恶劣天气频发、包车客运监管漏洞和农村交通繁忙等四个方面的挑战.全国公安交管部门要认清形势、正视问题,针对近期事故暴露出来的问题,强薄羽、补短板、堵漏洞,进一步推动五大行动,巩固扩大五大行动成果,全力确保冬季交通安全形势稳定.据此,某网站推出了关于交通道路安全情况的调查,通过调查年龄在![]() 的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%.现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组
的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%.现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求这100人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(2)现在要从年龄较大的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取2人进行问卷调查,求第2组恰好抽到1人的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过焦点且垂直于
,过焦点且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 所截得的弦长为
所截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 是坐标原点,求
是坐标原点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.

(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为了了解“微信支付”与“支付宝支付”的情况(“微信支付”与“支付宝支付”统称为“移动支付”),对消费者在该超市在2019年1-6月的支付方式进行统计,得到如图所示的折线图,则下列判断正确的是( )
①这6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多
②这6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大
③这6个月中4月份平均每天使用“移动支付”的次数最多
④2月份平均每天使用“移动支付”比5月份平均每天使用“移动支付”的次数多
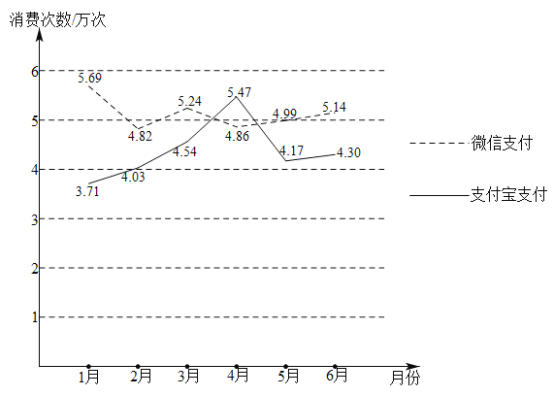
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱ABCA1B1C1中,已知AB=1,AA1=2,E,F,G分别是棱AA1,AC和A1C1的中点,以![]() 为正交基底,建立如图所示的空间直角坐标系F-xyz.
为正交基底,建立如图所示的空间直角坐标系F-xyz.

(1)求异面直线AC与BE所成角的余弦值;
(2)求二面角F-BC1-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com