(本题满分14分)设
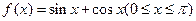
(1)求
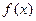
的最大值及
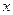
的值;(2)求

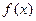
的单调区间;(3)若
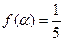
,求
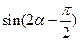
的值.
(1)

2分
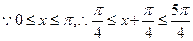
3分
所以当
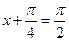
,即

时4分
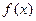
有最大值
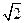
5分
(2)当
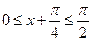
时
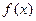
单调增, 6分当
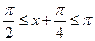
时
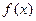
单调减, 7分
所以
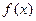
的单调增区间是
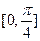
,单调减区间是
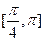
8分
(3)
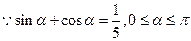
,
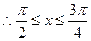
9分
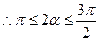
10分
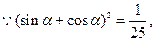
11分
所以
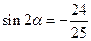
12分
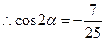
13分
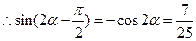
14分
或解:
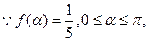
即
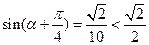
9分
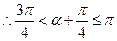
10分
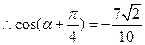
11分
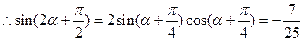
, 12分
即
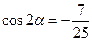
13分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题12分)设函数
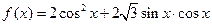
,
(I)求
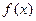
的最小正周期以及单调增区间;
(II)当
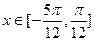
时,求
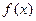
的值域;
(Ⅲ)若
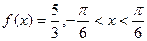
,求
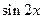
的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知函数

的图象过点

(Ⅰ)求
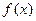
的解析式;
(Ⅱ)写出函数
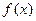
的图象是由函数
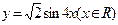
的图象经过怎样的变换得到的。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)(I)已知函数
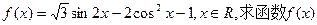
的最小正周期; (II)设
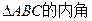
A、B、C的对边分别为a、b、c,且
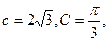
若向量
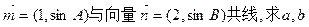
的值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
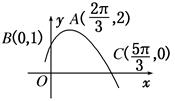
已知函数
f(
x)的部分图象如图所示,则
f(
x)的解析式可能为 ( )
| A.f(x)=2sin(+) | B.f(x)=sin(4x+) |
| C.f(x)=2sin(-) | D.f(x)=sin(4x-) |
查看答案和解析>>

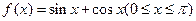 (1)求
(1)求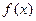 的最大值及
的最大值及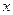 的值;(2)求
的值;(2)求
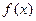 的单调区间;(3)若
的单调区间;(3)若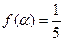 ,求
,求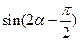 的值.
的值. 阅读快车系列答案
阅读快车系列答案