
【题目】已知函数![]() .
.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(III)在(II)的条件下,对任意的![]() ,求证:
,求证:![]() .
.
【答案】(I)当![]() 时,
时,![]() 在
在![]() 上单调递增,无单调递减区间,当
上单调递增,无单调递减区间,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(II)
;(II)![]() ;(III)证明见解析.
;(III)证明见解析.
【解析】试题分析:(I)利用![]() 时
时![]() 为单调增函数,
为单调增函数,![]() 时
时![]() 为单调减函数这一性质来分情况讨论题中
为单调减函数这一性质来分情况讨论题中![]() 单调区间问题;(II)根据函数单调性与最值,若
单调区间问题;(II)根据函数单调性与最值,若![]() 在
在![]() 上恒成立,则函数的最大值小于或等于零.当
上恒成立,则函数的最大值小于或等于零.当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,说明
,说明![]() 时
时![]() ,不合题意舍去.当
,不合题意舍去.当![]() 时,
时,![]() 的最大值小于零.但
的最大值小于零.但![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 只能等于零.令
只能等于零.令![]() 即可求得答案;(III)首先将
即可求得答案;(III)首先将![]() 的表达式表达出来,化简转化为
的表达式表达出来,化简转化为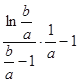 的形式,再根据(II)的结论得到
的形式,再根据(II)的结论得到![]() ,后逐步化简
,后逐步化简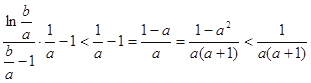 ,原命题得证.
,原命题得证.
试题解析:(I)![]() ,
,
当![]() 时,
时,![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上单调递增,无单调递减区间;
上单调递增,无单调递减区间;
当![]() 时,由
时,由![]() ,得
,得![]() ,由
,由![]() ,
,
得![]() ,此时
,此时![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(II)由(I)知:当![]() 时,
时,![]() 在
在![]() 上递增,
上递增,![]() ,显然不成立;
,显然不成立;
当![]() 时,
时,![]() ,只需
,只需![]() 即可,
即可,
令![]() ,则
,则![]() ,
,![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() .
.
![]() 对
对![]() 恒成立,也就是
恒成立,也就是![]() 对
对![]() 恒成立,
恒成立,
![]() ,解得
,解得![]() ,
,![]() 若
若![]() 在
在![]() 上恒成立,则
上恒成立,则![]() .
.
(III)证明: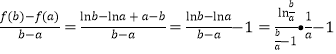 ,
,
由(II)得![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
又由![]() 得
得![]() ,所以有
,所以有![]() ,即
,即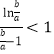 .
.
则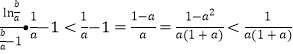 ,
,
则原不等式![]() 成立. ………(12分)
成立. ………(12分)


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知三棱锥P—ABC中,PC![]() 底面ABC,AB=BC,D、F分别为AC、PC的中点,DE
底面ABC,AB=BC,D、F分别为AC、PC的中点,DE![]() AP于E。(1)求证:AP
AP于E。(1)求证:AP![]() 平面BDE;(2)求证:平面BDE
平面BDE;(2)求证:平面BDE![]() 平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。
平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱锥P—ABC所成上、下两部分的体积比。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知函数f(x)(x∈R)是奇函数,且当x>0时,f(x)=2x-1,求函数f(x)的解析式.
(2)已知x+y=12,xy=9且x<y,求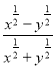 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三一次月考之后,为了为解数学学科的学习情况,现从中随机抽出若干名学生此次的数学成绩,按成绩分组,制成了下面频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
| 5 | 0.05 |
第二组 |
| 35 | 0.35 |
第三组 |
| 30 | 0.30 |
第四组 |
| 20 | 0.20 |
第五组 |
| 10 | 0.10 |
合计 | 100 | 1.00 | |
(1)试估计该校高三学生本次月考的平均分;
(2)如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率,那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩,并记成绩落在![]() 中的学生数为
中的学生数为![]() ,
,
求:①在三次抽取过程中至少有两次连续抽中成绩在![]() 中的概率;
中的概率;
②![]() 的分布列和数学期望.(注:本小题结果用分数表示)
的分布列和数学期望.(注:本小题结果用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={x|a+1≤x≤2a+1},Q={x|1≤2x+5≤15}.
(1)已知a=3,求(RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com