
【题目】(本小题满分12分)已知数列{an}是等差数列,且a1,a2(a1<a2)分别为方程x2﹣6x+5=0的二根.
(1)求数列{an}的前n项和Sn;
(2)在(1)中,设bn=![]() ,求证:当c=﹣
,求证:当c=﹣![]() 时,数列{bn}是等差数列.
时,数列{bn}是等差数列.
科目:高中数学 来源: 题型:
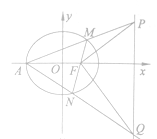
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 为该椭圆的右焦点,过点
为该椭圆的右焦点,过点![]() 任作一直线
任作一直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]() 的最大值为4.
的最大值为4.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,求证:
两点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式-2<|x-1|-|x+2|<0的解集为M ,a,b∈M .
(Ⅰ)证明:|![]() |<
|<![]() ;
;
(Ⅱ)比较|1-4ab|与2|a-b|的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点A(x , y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是 ![]() ,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A.[0,1]
B.[1,7]
C.[7,12]
D.[0,1]和[7,12]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床价高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结账,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入).
(1)把y表示成x的函数,并求出其定义域;
(2)试确定该宾馆将床位定价为多少时,既符合上面的两个条件,又能使净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分层抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法;在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱多少衰出之,问各几何?”其译文为:今有甲持560钱,乙持350钱,丙持180钱,甲、乙、丙三人一起出关,关税共100钱,要按照各人带钱多少的比例进行交税,问三人各应付多少税?则下列说法错误的是( )
A. 甲应付![]() 钱 B. 乙应付
钱 B. 乙应付![]() 钱
钱
C. 丙应付![]() 钱 D. 三者中甲付的钱最多,丙付的钱最少
钱 D. 三者中甲付的钱最多,丙付的钱最少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的正切值
B.人的右手一柞长和身高
C.正方体的棱长和表面积
D.真空中自由落体运动物体的下落距离和下落时间
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生完成数学作业所需时间,某学校统计了高三年级学生每天完成数学作业的平均时间介于30分钟到90分钟之间,图5是统计结果的频率分布直方图.

(1)数学教研组计划对作业完成较慢的20%的学生进行集中辅导,试求每天完成数学作业的平均时间为多少分钟以上的学生需要参加辅导?
(2)现从高三年级学生中任选4人,记4人中每天完成数学作业的平均时间不超过50分钟的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+ax2﹣4在x=2处取得极值,若m,n∈[0,1],则f'(n)+f(m)的最大值是( )
A.﹣9
B.﹣1
C.1
D.﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com