【答案】
分析:(Ⅰ)设直线l与曲线C相切于点P(x
,y
),利用导数的几何意义可得f′(x
)=5即可解得切点的横坐标x
,进而得到切点坐标及m的值;
(Ⅱ)解法一:由m∈Z,可得m=13,设h(x)=f(x)-g(x),则存在x∈[0,+∞)使f(x)≤g(x)成立?h(x)
min≤0,利用导数和分类讨论即可得出
解法二:由f(x)≤g(x)得
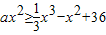
,
(ⅰ)当x≠0时,通过分离参数可得:
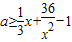
,设
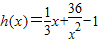
,则存在x∈[0,+∞)使f(x)≤g(x)成立?h(x)
min≤a,利用导数即可得出;
(ⅱ)当x=0时,不等式
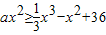
不成立,可知:a不存在.
解答:解:(Ⅰ)设直线l与曲线C相切于点P(x
,y
),
∵f'(x)=x
2-2x+2,∴
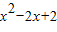
=5,解得x
=-1或x
=3,
当x
=-1时,y
=-1,∵P(-1,-1)在曲线C上,∴

,
当x
=3时,y
=19,∵P(3,19)在曲线C上,∴m=13,
∴切点P(-1,-1),
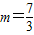
,
切点P(3,19),m=13.
(Ⅱ)解法一:∵m∈Z,∴m=13,
设
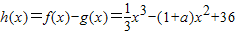
,
若存在x∈[0,+∞)使f(x)≤g(x)成立,则只要h(x)
min≤0,
h'(x)=x
2-2(1+a)x=x[x-2(1+a)],
(ⅰ)若1+a≥0即a≥-1,令h'(x)>0,得x>2(1+a)或x<0,
∵x∈[0,+∞),∴h(x)在(2(1+a),+∞)上是增函数,
令h'(x)≤0,解得0≤x≤2(1+a),
∴h(x)在[0,2(1+a)]上是减函数,∴h(x)
min=h(2(1+a)),
令h(2(1+a))≤0,解得a≥2,
(ⅱ)若1+a<0即a<-1,令h'(x)>0,解得x<2(1+a)或x>0,
∵x∈[0,+∞),∴h(x)在(0,+∞)上是增函数,∴h(x)
min=h(0),
令h(0)≤0,不等式无解,∴a不存在,
综合(ⅰ)(ⅱ)得,实数a的取值范围为[2,+∞).
解法二:由f(x)≤g(x)得
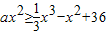
,
(ⅰ)当x≠0时,
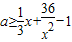
,设
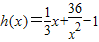
若存在x∈[0,+∞)使f(x)≤g(x)成立,则只要h(x)
min≤a,
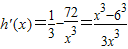
,
令h'(x)≥0解得x≥6,∴h(x)在[6+∞)上是增函数,
令h'(x)<0,解得0<x<6,∴h(x)在(0,6)上是减函数,
∴h(x)
min=h(6)=2,∴a≥2,
(ⅱ)当x=0时,不等式
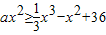
不成立,
∴a不存在,
综合(ⅰ)(ⅱ)得,实数a的取值范围为[2,+∞).
点评:熟练掌握利用导数研究函数的单调性、极值与最值、导数的几何意义、把问题等价转化等是解题的关键.

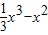 +2x+m的一条切线,g(x)=ax2+2x-23.
+2x+m的一条切线,g(x)=ax2+2x-23.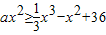 ,
,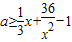 ,设
,设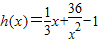 ,则存在x∈[0,+∞)使f(x)≤g(x)成立?h(x)min≤a,利用导数即可得出;
,则存在x∈[0,+∞)使f(x)≤g(x)成立?h(x)min≤a,利用导数即可得出;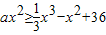 不成立,可知:a不存在.
不成立,可知:a不存在.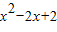 =5,解得x=-1或x=3,
=5,解得x=-1或x=3, ,
,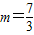 ,
,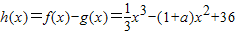 ,
,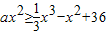 ,
,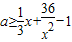 ,设
,设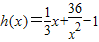
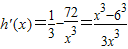 ,
,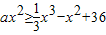 不成立,
不成立,
