
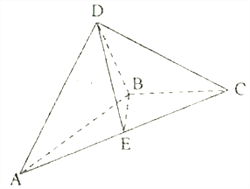
【题目】如图,在四面体![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,点
,点![]() 是
是![]() 的中点,求二面角
的中点,求二面角![]() 的大小.
的大小.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)由勾股定理可得![]() , 则
, 则![]() ,
,![]() ,进一步可得
,进一步可得![]() , 则
, 则![]() .
.
(Ⅱ)结合(Ⅰ)的结论和几何关系,以B为原点,建立空间直角坐标系![]() ,则平面BDE的法向量为
,则平面BDE的法向量为![]() ,且
,且![]() 是平面CBD的一个法向量.结合空间向量计算可得二面角
是平面CBD的一个法向量.结合空间向量计算可得二面角![]() 的大小为
的大小为![]() .
.
详解:(Ⅰ)由已知得![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
(Ⅱ)由(Ⅰ)知,AB与平面BCD所成的角为![]() ,即
,即![]() ,
,
设BD=2,则BC=2,在![]() 中,AB=4,
中,AB=4,
由(Ⅰ)中![]() ,得平面ABC⊥平面ABD,在平面ABD内,过点B作
,得平面ABC⊥平面ABD,在平面ABD内,过点B作![]() ,则
,则![]() 平面ABC,以B为原点,建立空间直角坐标系
平面ABC,以B为原点,建立空间直角坐标系![]() ,
,
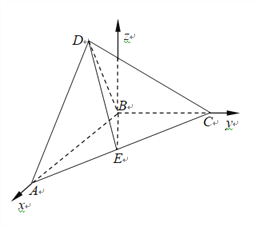
则![]() ,
,![]() ,
,![]() ,
,
![]() ,由
,由![]() ,
,
![]() ,
,
得![]() ,
,
∴![]() ,
,![]() ,
,
设平面BDE的法向量为![]() ,
,
则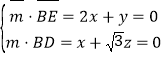 ,取
,取![]() ,解得
,解得![]() ,
,
∴![]() 是平面BDE的一个法向量,
是平面BDE的一个法向量,
又![]() 是平面CBD的一个法向量.
是平面CBD的一个法向量.
设二面角![]() 的大小为
的大小为![]() ,易知
,易知![]() 为锐角,
为锐角,
则![]() ,
,
∴![]() ,即二面角
,即二面角![]() 的大小为
的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
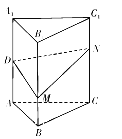
【题目】如图,正三棱柱![]() 的各条棱长均相等,
的各条棱长均相等, ![]() 为
为![]() 的中点,
的中点, ![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )
A. 平面![]() 平面
平面![]() B. 三棱锥
B. 三棱锥![]() 的体积为定值
的体积为定值
C. ![]() 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
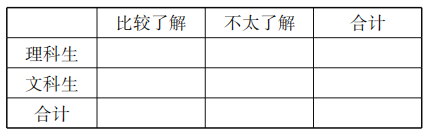
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:

(1)完成如下![]() 列联表,并判断是否有99%的把握认为,了解阿基米德与选择文理科有关?
列联表,并判断是否有99%的把握认为,了解阿基米德与选择文理科有关?
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(ⅰ)求抽取的文科生和理科生的人数;
(ⅱ)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.参考数据:
的分布列和数学期望.参考数据:

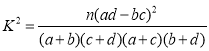 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才,对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:

例如,表中运动协调能力良好且逻辑思维能力一般的学生有![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
(III)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,设运动协调能力或逻辑思维能力优秀的学生人数为
位,设运动协调能力或逻辑思维能力优秀的学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 也为抛物线
也为抛物线![]() 的焦点,点
的焦点,点![]() 为
为![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)延长![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,求三角形
,求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 交于
交于![]() 不同两点分别过点
不同两点分别过点![]() 、点
、点![]() 作抛物线
作抛物线![]() 的切线,所得的两条切线相交于点
的切线,所得的两条切线相交于点![]() .
.
(Ⅰ)求证![]() 为定值:
为定值:
(Ⅱ)求![]() 的面积的最小值及此时的直线
的面积的最小值及此时的直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com