
【题目】已知函数![]() .
.
(1)证明![]() 在区间
在区间![]() 内有且仅有唯一实根;
内有且仅有唯一实根;
(2)记![]() 在区间
在区间![]() 内的实根为
内的实根为![]() ,函数
,函数![]() ,若方程
,若方程![]() 在区间
在区间![]() 有两不等实根
有两不等实根![]() ,证明
,证明![]() .
.
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,
,![]() ,第二组
,第二组![]() ,
,![]() ,
,![]() 第八组
第八组![]() ,
,![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() ;坐标系与参数方程
;坐标系与参数方程
在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为:
轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为:![]() .
.
(Ⅰ)将极坐标方程化为普通方程;
(Ⅱ)若点P(x,y)在该圆上,求x+y的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元,甲、乙电视台的广告费标准分别是500元/分钟和200元分钟,假设甲、乙两个电视台为该公司做的广告能给公司带来的收益分别为0.4万元/分钟和0.2万元分钟,那么该公司合理分配在甲、乙两个电视台的广告时间,能使公司获得最大的收益是()万元
A.72B.80C.84D.90
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次田径比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示。

若将运动员按成绩由好到差编为1—35号,再用系统抽样方法从中抽取5人,则其中成绩在区间![]() 上的运动员人数为
上的运动员人数为
A.6B.5C.4D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下表:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计我校7000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
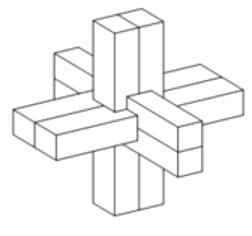
【题目】鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,从外表上看,六根等长的正四棱柱分成三组,经![]() 榫卯起来,如图,若正四棱柱的高为
榫卯起来,如图,若正四棱柱的高为![]() ,底面正方形的边长为
,底面正方形的边长为![]() ,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为( )(容器壁的厚度忽略不计)
,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为( )(容器壁的厚度忽略不计)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游胜地欲开发一座景观山,从山的侧面进行勘测,迎面山坡线![]() 由同一平面的两段抛物线组成,其中
由同一平面的两段抛物线组成,其中![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向下,
为顶点、开口向下,![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向上,以过山脚(点
为顶点、开口向上,以过山脚(点![]() )的水平线为
)的水平线为![]() 轴,过山顶(点
轴,过山顶(点![]() )的铅垂线为
)的铅垂线为![]() 轴建立平面直角坐标系如图(单位:百米).已知
轴建立平面直角坐标系如图(单位:百米).已知![]() 所在抛物线的解析式
所在抛物线的解析式![]() ,
,![]() 所在抛物线的解析式为
所在抛物线的解析式为![]()
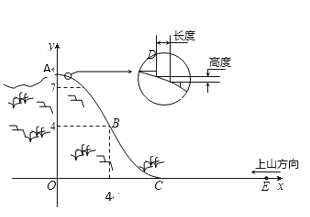
(1)求![]() 值,并写出山坡线
值,并写出山坡线![]() 的函数解析式;
的函数解析式;
(2)在山坡上的700米高度(点![]() )处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点
)处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点![]() 处,
处,![]() (米),假设索道
(米),假设索道![]() 可近似地看成一段以
可近似地看成一段以![]() 为顶点、开口向上的抛物线
为顶点、开口向上的抛物线![]() 当索道在
当索道在![]() 上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
(3)为了便于旅游观景,拟从山顶开始、沿迎面山坡往山下铺设观景台阶,台阶每级的高度为20厘米,长度因坡度的大小而定,但不得少于20厘米,每级台阶的两端点在坡面上(见图).试求出前三级台阶的长度(精确到厘米),并判断这种台阶能否一直铺到山脚,简述理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com