
【题目】如图,底面半径为![]() ,母线长为
,母线长为![]() 的圆柱的轴截面是四边形
的圆柱的轴截面是四边形![]() ,线段
,线段![]() 上的两动点
上的两动点![]() ,
, ![]() 满足
满足![]() .点
.点![]() 在底面圆
在底面圆![]() 上,且
上,且![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)四棱锥![]() 的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)要证线面平行,考虑到Q是AP的中点,因此可再取PB的中点H,从而由中位线定理得HQ与EF平行且相等,因此有FQ//HE,从而得线面平行;
(2)P点是固定的,平面ABCD是不变的,因此四棱锥的高是定值,而四棱锥的底面ABEF的面积也是不变的,因此体积为定值,由体积公式可得体积.
试题解析:
(1)证明:设PB的中点为F,连接HE,HQ,
在△ABP中,利用三角形中位线的性质可得QH∥AB,且QH=![]() AB,
AB,
又EF∥AB,EF=![]() AB,所以EF∥HQ,EF=HQ,
AB,所以EF∥HQ,EF=HQ,
所以四边形EFQH为平行四边形,所以FQ∥HE,
![]() 所以FQ∥平面BPE.
所以FQ∥平面BPE.
(2)四棱锥PABEF的体积为定值,定值为![]() .理由如下:
.理由如下:
由已知可得梯形ABEF的高为2,所以S梯形ABEF=![]() ×2=3,
×2=3,
又平面ABCD⊥平面ABP,过点P向AB作垂线PG,垂足为G,
则由面面垂直的性质定理可得PG⊥平面ABCD,
又AP=![]() ,AB=2,∠APB=90°,所以BP=1,
,AB=2,∠APB=90°,所以BP=1,
所以PG=![]() =
=![]() ,所以V四棱锥PABEF=
,所以V四棱锥PABEF=![]() ×PG×S梯形ABEF=
×PG×S梯形ABEF=![]() ×
×![]() ×3=
×3=![]() ,
,
所以四棱锥PABEF的体积为定值,定值为![]()


科目:高中数学 来源: 题型:
【题目】如图,已知长方体![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 垂直
垂直![]() 于点
于点![]() 为
为![]() 的中点.
的中点.
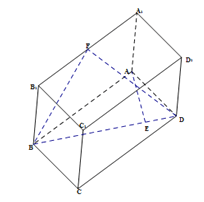
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 点位置;若不存在,说明理由.
点位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且过点
的焦点重合,且过点![]() .过点
.过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 为椭圆的左顶点.
为椭圆的左顶点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中
六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中![]() ,各踢了
,各踢了![]() 场,
场, ![]() 各踢了
各踢了![]() 场,
场, ![]() 踢了
踢了![]() 场,且
场,且![]() 队与
队与![]() 队未踢过,
队未踢过, ![]() 队与
队与![]() 队也未踢过,则在第一周的比赛中,
队也未踢过,则在第一周的比赛中, ![]() 队踢的比赛的场数是( )
队踢的比赛的场数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点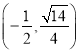 ,且离心率为
,且离心率为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 的右顶点,探究:
的右顶点,探究: ![]() 是否为定值,若是,求出该定值,若不是,请说明理由.(其中,
是否为定值,若是,求出该定值,若不是,请说明理由.(其中, ![]() ,
, ![]() 分别是直线
分别是直线![]() 、
、![]() 的斜率)
的斜率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个桔柚(球形水果)种植基地,已知所有采摘的桔柚的直径都在![]() 范围内(单位:毫米,以下同),按规定直径在
范围内(单位:毫米,以下同),按规定直径在![]() 内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:
内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:

(1)根据以上统计数据完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 以上的把握认为“桔柚直径与所在基地有关”?
以上的把握认为“桔柚直径与所在基地有关”?
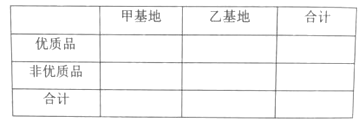
(2)求优质品率较高的基地的500个桔柚直径的样本平均数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(3)记甲基地直径在![]() 范围内的五个桔柚分别为
范围内的五个桔柚分别为![]() ,现从中任取二个,求含桔柚
,现从中任取二个,求含桔柚![]() 的概率.
的概率.
附: 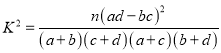 ,
, ![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,记随机变量
个,记随机变量![]() 表示质量在
表示质量在![]() 内的芒果个数,求
内的芒果个数,求![]() 的分布列及数学期望.
的分布列及数学期望.
(2)以各组数据的中间数代表这组数据的平均值,将频率视为概率,某经销商来收购芒果,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com