
(1)画出f(x)的图像;
(2)根据图像写出函数f(x)的单调区间;
(3)利用定义证明函数f(x)=-x2+2x+3在区间(-∞,1]上是增函数;
(4)当函数f(x)在区间(-∞,m]上是增函数时,求实数m的取值范围.
思路分析:本题主要考查二次函数的图像、函数的单调性及其综合应用.(1)画二次函数的图像时,重点确定开口方向和对称轴的位置;(2)根据单调性的几何意义,写出单调区间;(3)证明函数的增减性,先在区间上取x1<x2,然后作差f(x1)-f(x2),判断这个差的符号即可;(4)讨论对称轴和区间[m,+∞)的相对位置.
解:(1)函数f(x)=-x2+2x+3的图像如下图所示.
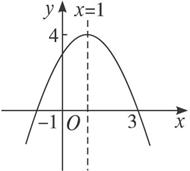
(2)由函数f(x)的图像,得在直线x=1的左侧图像是上升的,在直线x=1的右侧图像是下降的,故函数f(x)的单调递增区间是(-∞,1],单调递减区间是(1,+∞).
(3)设x1、x2∈(-∞,1],且x1<x2,则有
f(x1)-f(x2)=(-x12+2x1+3)-(-x22+2x2+3)
=(x22-x12)+2(x1-x2)
=(x1-x2)(2-x1-x2).
∵x1、x2∈(-∞,1],且x1<x2,
∴x1-x2<0,x1+x2<2.
∴2-x1-x2>0.
∴f(x1)-f(x2)<0.
∴f(x1)<f(x2).
∴函数f(x)=-x2+2x+3在区间(-∞,1]上是增函数.
(4)函数f(x)=-x2+2x+3的对称轴是直线x=1,在对称轴的左侧是增函数,那么当区间(-∞,m]位于对称轴的左侧时满足题意,则有m≤1,即实数m的取值范围是(-∞,1].
绿色通道:讨论二次函数的单调性时,要结合二次函数的图像,通过确定对称轴和单调区间的相对位置来解决.


科目:高中数学 来源: 题型:
|
| 1 |
| π |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-1 | x+a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com