
. |
| B |
. |
| A |
. |
| A |
. |
| B |
| A |
. |
| B |
. |
| B |
. |
| A |
. |
| A |
. |
| B |
| A |
. |
| B |


科目:高中数学 来源:学习周报 数学 北师大课标高一版(必修3) 2009-2010学年 第30期 总186期 北师大课标版 题型:044
甲、乙两名运动员在相同条件下各射靶10次,每次命中的环数分别是:
甲:8,6,7,8,6,5,9,10,4,7;
乙:6,7,7,8,6,7,8,7,9,5.
(1)分别计算以上两组数据的平均数;
(2)分别求出两组数据的方差;
(3)根据计算结果,估计一下甲、乙两名运动员的射击情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下:
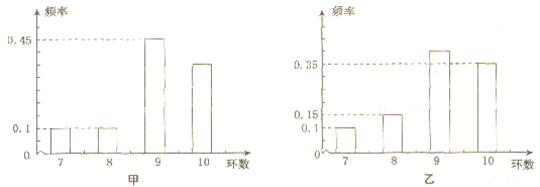
若将频率视为概率,回答下列问题.(Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率; (Ⅱ)若甲、乙两运动员各自射击1次,ξ表示这2次射击中击中9环以上(含9环)的次数,求ξ的分布列及Eξ.
查看答案和解析>>
科目:高中数学 来源:2012届四川省成都外国语学校高三8月月考数学 题型:解答题
(本小题满分12分)
(理)已知甲,乙两名射击运动员各自独立地射击1次,命中10环的概率分别为 ,x(x>
,x(x> );且乙运动员在2次独立射击中恰有1次命中10环的概率为
);且乙运动员在2次独立射击中恰有1次命中10环的概率为
(I)求x的值
(II)若甲,乙两名运动员各自独立地射击1次,设两人命中10环的次数之和为随机变量ξ,求ξ的分布列及数学期望
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省高三8月月考数学 题型:解答题
(本小题满分12分)
(理)已知甲,乙两名射击运动员各自独立地射击1次,命中10环的概率分别为 ,x(x>
,x(x> );且乙运动员在2次独立射击中恰有1次命中10环的概率为
);且乙运动员在2次独立射击中恰有1次命中10环的概率为
(I)求x的值
(II)若甲,乙两名运动员各自独立地射击1次,设两人命中10环的次数之和为随机变量ξ,求ξ的分布列及数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
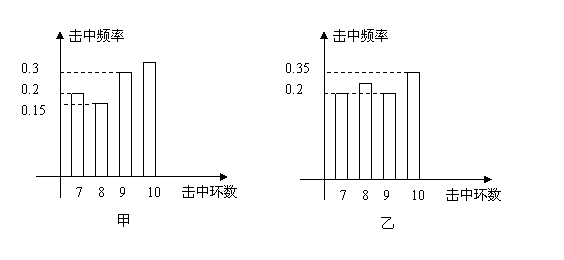
甲、乙两射击运动员进行射击比赛,射击次数相同,已知两运动员击中的环数![]() 稳定在7,8,9,10环,他们比赛成绩的频率分布条形图如下:(如果将频率近似的看作概率)
稳定在7,8,9,10环,他们比赛成绩的频率分布条形图如下:(如果将频率近似的看作概率)
(I)估计乙运动员击中8环的概率,并求甲、乙同时击中9环以上(包括9环)的概率.
(II)求甲运动员击中环数![]() 的概率分布列及期望;若从甲、乙运动员中只能挑选一名参加某大型比赛,你认为让谁参加比较合适?
的概率分布列及期望;若从甲、乙运动员中只能挑选一名参加某大型比赛,你认为让谁参加比较合适?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com