
【题目】执行如图所示的程序框图,若输入的x为4,则运行的次数与输出x的值分别为( ) 
A.5.730
B.5.729
C.4.244
D.4.243
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】已知点A(0,0),若函数f(x)的图象上存在两点B、C到点A的距离相等,则称该函数f(x)为“点距函数”,给定下列三个函数:①y=﹣x+2;② ![]() ;③y=x+1.其中,“点距函数”的个数是( )
;③y=x+1.其中,“点距函数”的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE. 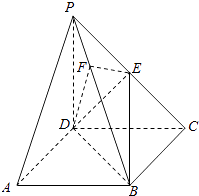
(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若面DEF与面ABCD所成二面角的大小为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,D为BC的中点,∠BAD+∠C≥90°. (Ⅰ)求证:sin2C≤sin2B;
(Ⅱ)若cos∠BAD=﹣ ![]() ,AB=2,AD=3,求AC.
,AB=2,AD=3,求AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】17世纪日本数学家们对这个数学关于体积方法的问题还不了解,他们将体积公式“V=kD3”中的常数k称为“立圆术”或“玉积率”,创用了求“玉积率”的独特方法“会玉术”,其中,D为直径,类似地,对于等边圆柱(轴截面是正方形的圆柱叫做等边圆柱)、正方体也有类似的体积公式V=kD3 , 其中,在等边圆柱中,D表示底面圆的直径;在正方体中,D表示棱长,假设运用此“会玉术”,求得的球、等边圆柱、正方体的“玉积率”分别为k1 , k2 , k3=( )
A.![]() :
: ![]() :1
:1
B.![]() :
: ![]() :2
:2
C.1:3: ![]()
D.1: ![]() :
: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC= ![]() ,点E在AD上,且AE=2ED. (Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
,点E在AD上,且AE=2ED. (Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
(Ⅱ)当二面角A﹣PB﹣E的余弦值为多少时,直线PC与平面PAB所成的角为45°?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣2ax,a∈R.
(1)若函数y=f(x)存在与直线2x﹣y=0平行的切线,求实数a的取值范围;
(2)设g(x)=f(x)+ ![]() ,若g(x)有极大值点x1 , 求证:
,若g(x)有极大值点x1 , 求证: ![]() >a.
>a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com