
【题目】设函数![]() 若函数
若函数![]() 的图象与
的图象与![]() 轴相邻两个交点间的距离为
轴相邻两个交点间的距离为![]() ,且图像的一条对称轴是直线
,且图像的一条对称轴是直线![]() 。
。
(1)求![]() 的值;
的值;
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)画出函数![]() 在区间
在区间![]() 上的图像。
上的图像。
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】自新冠肺炎疫情爆发后,各省纷纷派出医疗队支援湖北,全国上下凝聚一心,众志成城,终于取得抗疫胜利!小亮、小红、小金听闻支援湖北的“英雄”即将归来,各自独立完成一幅十字绣赠送给当地的医院,这三幅十字绣分别命名为“医者仁心”、“最美逆行者”、“德医双馨”,为了弄清作品都是谁制作的,院长对三人进行了问话,得到回复如下:小亮说:“最美逆行者”是我制作的;小红说:“医者仁心”不是小亮制作的,就是我制作的;小金说:“德医双馨”不是我制作的,若三人的说法有且仅有一人是正确的.通过以上信息判断,“最美逆行者”的制作者应该是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切正整数
,对一切正整数![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上,记
的图象上,记![]() 与
与![]() 的等差中项为
的等差中项为![]() 。
。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)设集合![]() ,等差数列
,等差数列![]() 的任意一项
的任意一项![]() ,其中
,其中![]() 是
是![]() 中的最小数,且
中的最小数,且![]() ,求
,求![]() 的通项公式。
的通项公式。
查看答案和解析>>
科目:高中数学 来源: 题型:
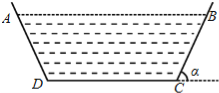
【题目】某地干旱少雨,农作物受灾严重,为了使今后保证农田灌溉,当地政府决定建一横断面为等腰梯形的水渠(水渠的横断面如图所示),为减少水的流失量,必须减少水与渠壁的接触面,若水渠横断面的面积设计为定值S,渠深为h,则水渠壁的倾斜角α(0<α<![]() )为多大时,水渠中水的流失量最小?
)为多大时,水渠中水的流失量最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2016 年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() 为常数),如果不搞促销活动,则该产品的年销售只能是
为常数),如果不搞促销活动,则该产品的年销售只能是![]() 万件.已知2016 年生产该产品的固定投入为
万件.已知2016 年生产该产品的固定投入为![]() 万元.每生产
万元.每生产![]() 万件该产品需要再投入
万件该产品需要再投入![]() 万元,厂家将每件产品的销售价格定为每件产品年平均成本的
万元,厂家将每件产品的销售价格定为每件产品年平均成本的![]() 倍(产品成本包括固定投入和再投入两部分资金).
倍(产品成本包括固定投入和再投入两部分资金).
(1)将2016 年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2016 年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间的关系,下表记录了小李某月连续5天每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出投篮命中率![]() 与打篮球时间
与打篮球时间![]() (单位:小时)之间的回归直线方程
(单位:小时)之间的回归直线方程![]() ;
;
(Ⅱ)如果小李某天打了2.5小时篮球,预测小李当天的投篮命中率.
(参考:用最小二乘法求线性回归方程系数公式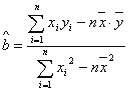 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm ( | 150 | 155 | 160 | 165 | 170 |
体重/kg ( | 43 | 46 | 49 | 51 | 56 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值![]() 为多少?
为多少?
参考公式:线性回归方程![]() ,其中
,其中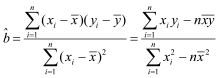 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
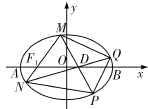
【题目】(本小题满分12分)如图,在平面直角坐标系![]() 中, 已知
中, 已知![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点
的左、右焦点![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为线段
为线段![]() 的中点, 且
的中点, 且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为椭圆
为椭圆![]() 上的动点(异于点
上的动点(异于点![]() ),连接
),连接![]() 并延长交椭圆
并延长交椭圆![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 并分别延
并分别延
长交椭圆![]() 于点
于点![]() 连接
连接![]() ,设直线
,设直线![]() 、
、![]() 的斜率存在且分别为
的斜率存在且分别为![]() 、
、![]() ,试问是否存在常数
,试问是否存在常数![]() ,使
,使
得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com