
| A. | $\frac{{2\sqrt{5}π}}{5}$ | B. | $\frac{{4\sqrt{5}π}}{5}$ | C. | $\frac{{2\sqrt{10}π}}{5}$ | D. | $\frac{{4\sqrt{10}π}}{5}$ |
分析 取BB1的中点H,连结CH,则CH⊥NB,DC⊥NB,可得NB⊥面DCH,即动点M的轨迹就是平面DCH与内切球O的交线,求得截面圆的半径r=$\sqrt{{R}^{2}-{d}^{2}}=\frac{2\sqrt{2}}{\sqrt{5}}$,动点M的轨迹的长度为截面圆的周长2πr
解答 解:如图,正方体ABCD-A1B1C1D1的内切球O的半径R=$\sqrt{2}$,由题意,取BB1的中点H,连结CH,则CH⊥NB,DC⊥NB,∴NB⊥面DCH,
∴动点M的轨迹就是平面DCH与内切球O的交线,∵正方体ABCD-A1B1C1D1的棱长是2$\sqrt{2}$,∴O到平面DCH的距离为d=$\frac{2}{\sqrt{5}}$,
截面圆的半径r=$\sqrt{{R}^{2}-{d}^{2}}=\frac{2\sqrt{2}}{\sqrt{5}}$,动点M的轨迹的长度为截面圆的周长2πr=$\frac{4\sqrt{10}}{5}$.
故选:D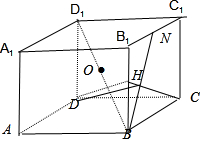
点评 本题考查了空间动点轨迹问题,弄清动点的轨迹是解题关键,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②④ | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2\sqrt{3},\sqrt{17})$ | B. | $(\sqrt{17},\sqrt{21})$ | C. | $(\sqrt{17},2\sqrt{6})$ | D. | $(\sqrt{21},2\sqrt{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$或$\sqrt{10}$ | B. | $\sqrt{10}$或$\frac{2\sqrt{2}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
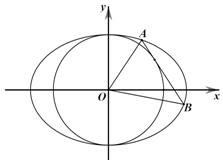 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{\;}}$=1(a>b>0)过点(0,1)和(1,$\frac{\sqrt{2}}{2}$),圆O:x2+y2=b2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com