Question

19．已知$\overrightarrow{OA}=（{4，-3}）$，将其绕原点O逆时针旋转120°后又伸长到原来的2倍得向量$\overrightarrow{OA'}$，则$\overrightarrow{OA'}$=（-4+3$\sqrt{3}$，3+4$\sqrt{3}$）．

Answer 1

分析 根据题意画出图形，结合图形设∠xOA=α，且α∈（0°，90°），则∠xOA′=120°-α，求出sinα、cosα；再求cos（120°-α）、sin（120°-α）的值，再求x=|$\overrightarrow{OA′}$|cos（90°-∠xOA′）和y=|$\overrightarrow{OA′}$|sin（90°-∠xOA′）的值，即可得出$\overrightarrow{OA′}$的坐标表示．

解答 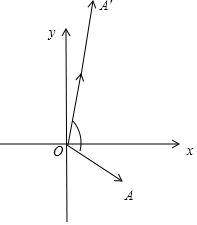解：∵$\overrightarrow{OA}=（{4，-3}）$，∴|$\overrightarrow{OA}$|=5，
将其绕原点O逆时针旋转120°后又伸长到原来的2倍得向量$\overrightarrow{OA'}$，
∴|$\overrightarrow{OA′}$|=2×5=10；
如图所示，
设∠xOA=α，且α∈（0°，90°），
则∠xOA′=120°-α，
且sin（-α）=$\frac{-3}{5}$，∴sinα=$\frac{3}{5}$＞$\frac{1}{2}$，∴30°＜α＜45°；
∴cos（-α）=cosα=$\frac{4}{5}$；
∴cos（120°-α）=cos120°cosα+sin120°sinα=-$\frac{1}{2}$×$\frac{4}{5}$+$\frac{\sqrt{3}}{2}$×$\frac{3}{5}$=$\frac{-4+3\sqrt{3}}{10}$，
sin（120°-α）=sin120°cosα-cos120°sinα=$\frac{\sqrt{3}}{2}$×$\frac{4}{5}$-（-$\frac{1}{2}$）×$\frac{3}{5}$=$\frac{4\sqrt{3}+3}{10}$；
∴x=|$\overrightarrow{OA′}$|cos（90°-∠xOA′）=10×$\frac{-4+3\sqrt{3}}{10}$=-4+3$\sqrt{3}$，
y=|$\overrightarrow{OA′}$|sin（90°-∠xOA′）=10×$\frac{4\sqrt{3}+3}{10}$=3+4$\sqrt{3}$，
∴$\overrightarrow{OA′}$=（-4+3$\sqrt{3}$，3+4$\sqrt{3}$）．
故答案为：$（{-4+3\sqrt{3}，3+4\sqrt{3}}）$．

点评 本本题考查了平面向量的旋转变换问题，也考查了三角函数的应用问题，解题时应用数形结合的思想，是综合题．