
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,若过两点
,若过两点![]() 的直线
的直线![]() 与
与![]() 轴的交点在曲线
轴的交点在曲线![]() 上,求
上,求![]() 的值.
的值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)当![]() 时,求得
时,求得![]() ,解得
,解得![]() ,
,![]() ,利用导数的几何意义,即可求解,得到答案.
,利用导数的几何意义,即可求解,得到答案.
(2)求得![]() ,由
,由![]() ,解得
,解得![]() ,
,![]() ,分类讨论,求得即可得到函数的单调性;
,分类讨论,求得即可得到函数的单调性;
(3)求得![]() ,由
,由![]() 为方程
为方程![]() 的两个根,求得
的两个根,求得![]() 及
及![]() ,进而求得
,进而求得![]() ,
,![]() ,得出两点
,得出两点![]() 在直线
在直线![]() 上,求得
上,求得![]() 与
与![]() 轴的交点为
轴的交点为![]() ,代入
,代入![]() ,即可求解.
,即可求解.
(1)由题意,当![]() 时,
时,![]() ,则
,则![]() ,可得
,可得![]() ,
,![]() ,
,
所以点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(2)由题意,得![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
①当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单增;
上单增;
②当![]() 时,
时,![]() .
.
|
|
|
|
|
|
| + | 0 | — | 0 | + |
| ↑ | 极大值 | ↓ | 极小值 | ↑ |
所以![]() 单增区间为
单增区间为![]() 和
和![]() ,单减区间为
,单减区间为![]() .
.
(3)由函数![]() ,则
,则![]() ,
,
由题设知![]() 为方程
为方程![]() 的两个根,故有
的两个根,故有![]() ,解得
,解得![]()
且![]()
![]()
![]() ,
,
同理![]() ,
,
所以两点![]() 在直线
在直线![]() 上,
上,
设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,得
,得![]() ,
,
由题设,点![]() 在曲线
在曲线![]() 上,
上,
所以![]()
解得![]() 或
或![]() 或
或![]() ,所以
,所以![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=4x的焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(﹣1,0).
(1)当l与x轴垂直时,求△ABM的外接圆方程;
(2)记△AMF的面积为S1,△BMF的面积为S2,当S1=4S2时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年,在庆祝中华人民共和国成立
年,在庆祝中华人民共和国成立![]() 周年之际,又迎来了以“创军人荣耀,筑世界和平”为宗旨的第七届世界军人运动会.据悉,这次军运会将于
周年之际,又迎来了以“创军人荣耀,筑世界和平”为宗旨的第七届世界军人运动会.据悉,这次军运会将于![]() 年
年![]() 月
月![]() 日至
日至![]() 日在美丽的江城武汉举行,届时将有来自全世界
日在美丽的江城武汉举行,届时将有来自全世界![]() 多个国家和地区的近万名军人运动员参赛.相对于奥运会、亚运会等大型综合赛事,军运会或许对很多人来说还很陌生.为此,武汉某高校为了在学生中更广泛的推介普及军运会相关知识内容,特在网络上组织了一次“我所知晓的武汉军运会”知识问答比赛,为便于对答卷进行对比研究,组委会抽取了
多个国家和地区的近万名军人运动员参赛.相对于奥运会、亚运会等大型综合赛事,军运会或许对很多人来说还很陌生.为此,武汉某高校为了在学生中更广泛的推介普及军运会相关知识内容,特在网络上组织了一次“我所知晓的武汉军运会”知识问答比赛,为便于对答卷进行对比研究,组委会抽取了![]() 名男生和
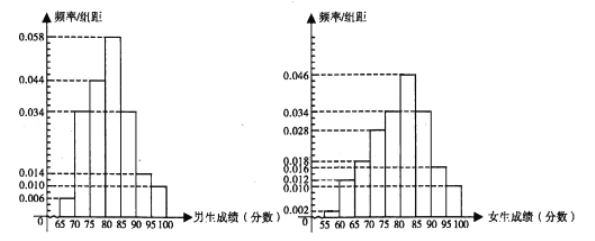
名男生和![]() 名女生的答卷,他们的考试成绩频率分布直方图如下:
名女生的答卷,他们的考试成绩频率分布直方图如下:
(注:问卷满分为![]() 分,成绩
分,成绩![]() 的试卷为“优秀”等级)
的试卷为“优秀”等级)
(1)从现有![]() 名男生和
名男生和![]() 名女生答卷中各取一份,分别求答卷成绩为“优秀”等级的概率;
名女生答卷中各取一份,分别求答卷成绩为“优秀”等级的概率;
(2)求列联表中![]() ,
,![]() ,
,![]() ,
,![]() 的值,并根据列联表回答:能否在犯错误的概率不超过
的值,并根据列联表回答:能否在犯错误的概率不超过![]() 的前提下认为“答卷成绩为优秀等级与性别有关”?
的前提下认为“答卷成绩为优秀等级与性别有关”?
男 | 女 | 总计 | |
优秀 |
|
|
|
非优秀 |
|
|
|
总计 |
|
|
|
(3)根据男、女生成绩频率分布直方图,对他们的成绩的优劣进行比较.
附:参考公式:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(请写出式子在写计算结果)有4个不同的小球,4个不同的盒子,现在要把球全部放入盒内:
(1)共有多少种方法?
(2)若每个盒子不空,共有多少种不同的方法?
(3)恰有一个盒子不放球,共有多少种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对在直角坐标系的第一象限内的任意两点![]() ,
,![]() 作如下定义:
作如下定义:![]() ,那么称点
,那么称点![]() 是点
是点![]() 的“上位点”,同时点
的“上位点”,同时点![]() 是点
是点![]() 的“下位点”.
的“下位点”.
(1)试写出点![]() 的一个“上位点”坐标和一个“下位点”坐标;
的一个“上位点”坐标和一个“下位点”坐标;
(2)设![]() 、
、![]() 、
、![]() 、
、![]() 均为正数,且点
均为正数,且点![]() 是点
是点![]() 的上位点,请判断点
的上位点,请判断点![]() 是否既是点
是否既是点![]() 的“下位点”又是点
的“下位点”又是点![]() 的“上位点”,如果是请证明,如果不是请说明理由;
的“上位点”,如果是请证明,如果不是请说明理由;
(3)设正整数![]() 满足以下条件:对任意实数
满足以下条件:对任意实数![]() ,总存在
,总存在![]() ,使得点
,使得点![]() 既是点
既是点![]() 的“下位点”,又是点
的“下位点”,又是点![]() 的“上位点”,求正整数
的“上位点”,求正整数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与圆
与圆![]() :
:![]() 有且仅有两个公共点,点
有且仅有两个公共点,点![]() 、
、![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 上的动点、左焦点、右焦点,三角形
上的动点、左焦点、右焦点,三角形![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在椭圆第一象限部分上运动,过点
在椭圆第一象限部分上运动,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,过点
,过点![]() 作
作![]() 的垂线
的垂线![]() ,求证:
,求证:![]() ,
,![]() 交点
交点![]() 的纵坐标的绝对值为定值.
的纵坐标的绝对值为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com