
【题目】在如图所示的圆台中,![]() 是下底面圆
是下底面圆![]() 的直径,
的直径,![]() 是上底面圆
是上底面圆![]() 的直径,
的直径,![]() 是圆台的一条母线.
是圆台的一条母线.
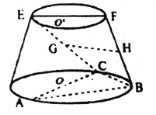
(Ⅰ)已知![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】
试题分析:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() ,推导出平面
,推导出平面![]() 平面
平面![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;(Ⅱ)由
;(Ⅱ)由![]() ,知
,知![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能求出二面角
轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,![]() ,
,![]() 、
、![]() 在上底面内,
在上底面内,![]() 不在上底面内,
不在上底面内,![]() 上底面,………………2分
上底面,………………2分
![]() 平面
平面![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,………………4分
,………………4分
所以平面![]() 平面
平面![]() ,由
,由![]() 平面
平面![]() ,
,![]() 平面
平面![]() .………………5分
.………………5分
(Ⅱ)连结![]() ,
,![]() ,
,![]() ,………………6分
,………………6分
以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,
于是有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得平面![]() 中的向量
中的向量![]() ,
,![]() ,于是得平面
,于是得平面![]() 的一个法向量
的一个法向量![]() ,………………9分
,………………9分
又平面![]() 的一个法向量
的一个法向量![]() ………………10分
………………10分
设二面角![]() 为
为![]() ,则
,则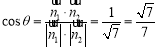 ,
,
二面角![]() 的余弦值为
的余弦值为![]() ………………12分
………………12分


科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,函数
时,函数![]() 与
与![]() 在
在![]() 处的切线互相垂直,求
处的切线互相垂直,求![]() 的值;
的值;
(2)若函数![]() 在定义域内不单调,求
在定义域内不单调,求![]() 的取值范围;
的取值范围;
(3)是否存在正实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 恒成立?若存在,求出满足条件的实数
恒成立?若存在,求出满足条件的实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,为了保护环境,实现城市绿化,某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC,建造住宅小区公园,但不能越过文物保护区三角形AEF的边线EF.已知AB=CD=200 m,BC=AD=160 m,AF=40 m,AE=60 m,问如何设计才能使公园占地面积最大,求出最大面积.
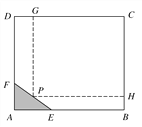
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产某种产品时的能耗y与产品件数x之间的关系式为y=ax+![]() .且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.
.且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.
(1)写出函数y关于x的解析式;
(2)用列表法表示此函数,并画出图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)满足f(2+x)=f(2-x),对于x∈R恒成立,且f(x)=0的两个实数根的平方和为10,f(x)的图象过点(0,3),求f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的右焦点与抛物线![]() 的焦点重合,点M
的焦点重合,点M![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)设![]() ,直线
,直线![]() 与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求
与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为梯形,
为梯形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
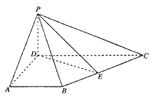
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com