
【题目】如图1,已知正方形铁片![]() 边长为2a米,四边中点分别为E,F,G,H,沿着虚线剪去大正方形的四个角,剩余为四个全等的等腰三角形和一个正方形ABCD(两个正方形中心重合且四边相互平行),沿正方形ABCD的四边折起,使E,F,G,H四点重合,记为P点,如图2,恰好能做成一个正四棱锥(粘贴损耗不计),PO⊥底面ABCD,O为正四棱锥底面中心,设正方形ABCD的边长为2x米.
边长为2a米,四边中点分别为E,F,G,H,沿着虚线剪去大正方形的四个角,剩余为四个全等的等腰三角形和一个正方形ABCD(两个正方形中心重合且四边相互平行),沿正方形ABCD的四边折起,使E,F,G,H四点重合,记为P点,如图2,恰好能做成一个正四棱锥(粘贴损耗不计),PO⊥底面ABCD,O为正四棱锥底面中心,设正方形ABCD的边长为2x米.
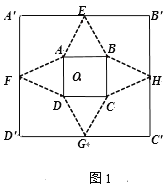
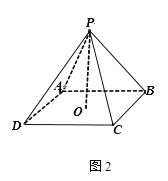
(1)若正四棱锥的棱长都相等,求所围成的正四棱锥的全面积S;
(2)请写出正四棱锥的体积V关于x的函数,并求V的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
. ![]() .
.
【解析】
(1)连接OH交BC于点H′,由正方形ABCD边长为2x,所以HH′=a-x.
可得![]() 的长及
的长及![]() 的长,由
的长,由![]() 得可得
得可得![]() 的值,可得正四棱锥的全面积
的值,可得正四棱锥的全面积![]() ,计算可得答案;
,计算可得答案;
(2)可得![]() ,可得
,可得![]() 关于
关于![]() 的函数,对其求导,利用导数可得V的最大值.
的函数,对其求导,利用导数可得V的最大值.
解:在图1中连接OH交BC于点H′,
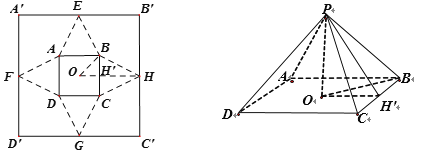
因为正方形ABCD边长为2x,所以HH′=a-x.
在图2中,OH′=x,PH′=a-x,
由勾股定理得,正四棱锥的高
![]()
![]() .
.
(1)在直角三角形![]() 中,
中,![]() ,
,
所以![]() ,
,
由![]() 得,
得,![]() ,
,
整理得,![]() ,解得
,解得![]() (
(![]() 舍去).
舍去).
所以,正四棱锥的全面积![]()
![]()
![]() 平方米.
平方米.
(2)![]() ,
,
所以![]() .
.
因为![]() ,设
,设![]() ,
,
则![]()
![]() ,
,
令![]() 得,
得,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递增;
上递增;
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递减.
上递减.
所以当![]() 时,
时,![]() 取得最大值,此时
取得最大值,此时![]() 立方米.
立方米.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】斐波那契数列![]() 满足:
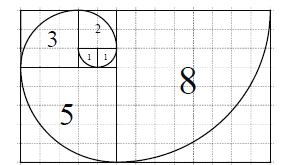
满足: ![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把活跃网店数量较多的村庄称为淘宝村,随着电子商务在中国的发展,不少农村出现了一批专业的淘宝村,已知某乡镇有多个淘宝村,现从该乡镇淘宝村中随机抽取![]() 家商户,统计他们某一周的销售收入,结果统计如下:
家商户,统计他们某一周的销售收入,结果统计如下:
销售收入(收入) |
|
|
|
|
商户数 |
|
|
|
|
(1)从这![]() 家商户中按该周销售收入超过
家商户中按该周销售收入超过![]() 万元与不超过
万元与不超过![]() 万元分为
万元分为![]() 组,按分层抽样从中抽取
组,按分层抽样从中抽取![]() 家参加经验交流会,并从这
家参加经验交流会,并从这![]() 家中选
家中选![]() 家进行发言,求选出的
家进行发言,求选出的![]() 家恰有
家恰有![]() 家销售收入超过
家销售收入超过![]() 万元的概率;
万元的概率;
(2)若这![]() 家商户中有
家商户中有![]() 家商户入驻两家网购平台,其中
家商户入驻两家网购平台,其中![]() 家销售收入高于
家销售收入高于![]() 万元,完成下面的
万元,完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“销售收入是否高于
的把握认为“销售收入是否高于![]() 万元与入驻两家网购平台有关”?
万元与入驻两家网购平台有关”?
入驻两家网购平台 | 仅入驻一家网购平台 | 合计 | |
销售收入高于 | |||
销售收入不高于 | |||
合计 |
附: .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
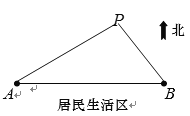
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试后,对全班同学的数学成绩进行整理,得到表:
分数段 |
|
|
|
|
人数 | 5 | 15 | 20 | 10 |
将以上数据绘制成频率分布直方图后,可估计出本次考试成绩的中位数是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点为
的两个焦点为![]() 、
、![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项,其中
的等差中项,其中![]() 、
、![]() 、
、![]() 都是正数,过点
都是正数,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
(1)求椭圆的方程;
(2)点![]() 是椭圆上一动点,定点
是椭圆上一动点,定点![]() ,求△
,求△![]() 面积的最大值;
面积的最大值;
(3)已知定点![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 相异两点.证明:对任意的
相异两点.证明:对任意的![]() ,都存在实数
,都存在实数![]() ,使得以线段
,使得以线段![]() 为直径的圆过
为直径的圆过![]() 点.
点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com