
【题目】若![]() (
(![]() )恰有1个零点,则实数
)恰有1个零点,则实数![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
令![]() 得到
得到![]() ,问题转化为函数
,问题转化为函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上恰有1个交点,用导数法作出
上恰有1个交点,用导数法作出![]() 的图像,根据图像求出直线与函数
的图像,根据图像求出直线与函数![]() 只有一个交点满足的条件,即可求出结论.
只有一个交点满足的条件,即可求出结论.
由![]() 恰有1个零点,方程
恰有1个零点,方程![]() 恰有1个解,即方程
恰有1个解,即方程![]() 恰有1个解,即函数
恰有1个解,即函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上恰有1个交点,因为
上恰有1个交点,因为![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 上都是减函数,在
上都是减函数,在![]() 是增函数,当
是增函数,当![]() 时,
时,![]() 取极小值
取极小值![]() ,直线
,直线![]() 过点
过点![]() ,斜率为
,斜率为![]() ,显然
,显然![]() 是函数
是函数![]() 的图象与直线
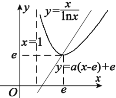
的图象与直线![]() 的一个交点,这两个图象不能有其他交点,作出函数
的一个交点,这两个图象不能有其他交点,作出函数![]() 与
与![]() 的图象,由图可知,当
的图象,由图可知,当![]() 时,直线
时,直线![]() 应在函数
应在函数![]() (
(![]() )的图象上方,
)的图象上方,
设![]() ,即
,即![]() 恒成立,因为
恒成立,因为![]() ,
,![]() 只需
只需![]() 为减函数,所以
为减函数,所以![]() ,即
,即![]() 恒成立,设
恒成立,设![]() ,设
,设![]() ,则
,则![]() ,
,![]()
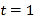 ,当且仅当
,当且仅当![]() ,即
,即![]() ,即
,即![]() ,
,
即![]() 时,
时,![]() ,所以
,所以![]() ,当
,当![]() 时,直线
时,直线![]() 与
与
![]() 相切,也适合,故满足题意
相切,也适合,故满足题意![]() 的取值范围为
的取值范围为![]() .
.
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且函数
,且函数![]() 在区间
在区间![]() 内有两个极值点,求实数a的取值范围;
内有两个极值点,求实数a的取值范围;
(3)求证:对任意的正数a,都存在实数t,满足:对任意的![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为实数.
为实数.
(1)当![]() 时,判断函数
时,判断函数![]() 在其定义域上的单调性;
在其定义域上的单调性;
(2)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,
,![]() 恒成立?若不存在,请说明理由;若存在,求出
恒成立?若不存在,请说明理由;若存在,求出![]() 的值并加以证明.
的值并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
假设客户是否满意互相独立,且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等.
(1)从所有的回访客户中随机抽取1人,求这个客户满意的概率;
(2)从I型号和V型号汽车的所有客户中各随机抽取1人,设其中满意的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)用 “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”分别表示I, II, III, IV, V型号汽车让客户满意, “
”分别表示I, II, III, IV, V型号汽车让客户满意, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差
” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 义乌国际马拉松赛,某校要从甲乙丙丁等
义乌国际马拉松赛,某校要从甲乙丙丁等![]() 人中挑选
人中挑选![]() 人参加比赛,其中甲乙丙丁
人参加比赛,其中甲乙丙丁![]() 人中至少有
人中至少有![]() 人参加且甲乙不同时参加,丙丁也不同时参加,则不同的报名方案有( )
人参加且甲乙不同时参加,丙丁也不同时参加,则不同的报名方案有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁可以得到2张A2纸,依此类推.这是因为A系列纸张的长宽比为![]() :1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈![]() ,那么A4纸的长度为( )
,那么A4纸的长度为( )
A.![]() 厘米B.
厘米B.![]() 厘米C.
厘米C.![]() 厘米D.
厘米D.![]() 厘米
厘米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100名学生,其中阅读过《西游记》的学生有70位,只阅读过《红楼梦》的学生有20位,则既没阅读过《西游记》也没阅读过《红楼梦》的学生人数与该校学生总数比值的估计值为( )
A.0.1B.0.2C.0.3D.0.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com