[题目]已知条件p:-1≤x≤10.q:x2-4x+4-m2≤0(m>0)不变.若 p是 q的必要而不充分条件.如何求实数m的取值范围? 题目和参考答案——青夏教育精英家教网—

【题目】已知条件p：－1≤x≤10，q：x2－4x＋4－m2≤0(m>0)不变，若 p是 q的必要而不充分条件，如何求实数m的取值范围？

【答案】【解答】p：－1≤x≤10.
q：x2－4x＋4－m2≤0
[x－(2－m)][x－(2＋m)]≤0(m>0)
2－m≤x≤2＋m(m>0)．
因为 p是 q的必要而不充分条件，
所以p是q的充分不必要条件，
即{x|－1≤x≤10} {x|2－m≤x≤2＋m}，
故有或解得m≥8.所以实数m的范围为{m|m≥8}．
【解析】对于结论中含有参数问题，可先将其转化为最简形式，利用充分条件、必要条件或充要条件揭示命题和结论之间的从属关系，借助于Venn图或数轴的直观性列方程或不等式，即可求出参数的值或取值范围．

练习册系列答案

中考夺标全国各省市中考试题分类系列答案

星空小学假期作业寒假乐园新疆青少年出版社系列答案

快乐假期寒假作业延边教育出版社系列答案

易考教育书系中考导航中考试卷汇编系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设f（x）=ax3+bx2+cx的极小值为﹣8，其导函数y=f′（x）的图象经过点，如图所示，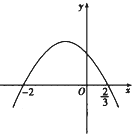
（1）求f（x）的解析式；
（2）若对x∈[﹣3，3]都有f（x）≥m2﹣14m恒成立，求实数m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对于函数f（x）定义域中任意的x1 ， x2（x1≠x2）有如下结论
1）f（x1+x2）=f（x1）f（x2）
2）f（x1x2）=f（x1）+f（x2）
3）＞0
4）f（）＜
5）f（）＞
6）f（﹣x）=f（x）．
当f（x）=lgx时，上述结论正确的序号为．（注：把你认为正确的命题的序号都填上）．