
【题目】为了预防新型冠状病毒的传染,人员之间需要保持一米以上的安全距离.某公司会议室共有四行四列座椅,并且相邻两个座椅之间的距离超过一米,为了保证更加安全,公司规定在此会议室开会时,每一行、每一列均不能有连续三人就座.例如下图中第一列所示情况不满足条件(其中“√”表示就座人员).根据该公司要求,该会议室最多可容纳的就座人数为( )
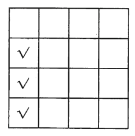
A.9B.10C.11D.12
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,5,11,21,37,6l,95,则该数列的第8项为( )
A.99B.131C.139D.141
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点.对任意的点
为坐标原点.对任意的点![]() ,定义
,定义![]() .任取点
.任取点![]() ,
,![]() ,记
,记![]() ,
,![]() ,若此时
,若此时![]() 成立,则称点
成立,则称点![]() ,
,![]() 相关.
相关.
(1)分别判断下面各组中两点是否相关,并说明理由;
①![]() ,
,![]() ;②
;②![]() ,
,![]() .
.
(2)给定![]() ,
,![]() ,点集
,点集![]() .
.
(![]() )求集合
)求集合![]() 中与点
中与点![]() 相关的点的个数;
相关的点的个数;
(![]() )若
)若![]() ,且对于任意的
,且对于任意的![]() ,
,![]() ,点
,点![]() ,
,![]() 相关,求
相关,求![]() 中元素个数的最大值.
中元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播、微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男、女学生,发现有![]() 的男生喜欢网络课程,有
的男生喜欢网络课程,有![]() 的女生不喜欢网络课程,且有
的女生不喜欢网络课程,且有![]() 的把握但没有
的把握但没有![]() 的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
附: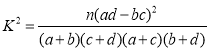 ,其中
,其中![]() .
.
|
|
|
|
|
k |
|
|
|
|
A.130B.190C.240D.250
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等腰梯形ABCD中,AB∥CD,AD=AB=BC=1,CD=2,E为CD中点,以AE为折痕把△ADE折起,使点D到达点P的位置(P平面ABCE).
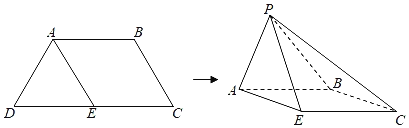
(1)证明:AE⊥PB;
(2)若直线PB与平面ABCE所成的角为![]() ,求二面角A﹣PE﹣C的余弦值.
,求二面角A﹣PE﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com