
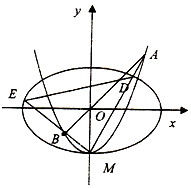
 ШчЭМЃЌЭждВC1ЃК$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЃЈaЃОbЃО0ЃЉЕФРыаФТЪЮЊ$\frac{\sqrt{2}}{2}$ЃЌxжсБЛЧњЯпC2ЃКy=x2-bНиЕУЕФЯпЖЮГЄЕШгкC1ЕФЖЬжсГЄЃЌC2гыyжсЕФНЛЕуЮЊMЃЌЙ§зјБъдЕуOЕФжБЯпlгыC2ЯрНЛгкЕуAЁЂBЃЌжБЯпMAЃЌMBЗжБ№гыC1ЯрНЛгкЕуDЁЂEЃЎ
ШчЭМЃЌЭждВC1ЃК$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1ЃЈaЃОbЃО0ЃЉЕФРыаФТЪЮЊ$\frac{\sqrt{2}}{2}$ЃЌxжсБЛЧњЯпC2ЃКy=x2-bНиЕУЕФЯпЖЮГЄЕШгкC1ЕФЖЬжсГЄЃЌC2гыyжсЕФНЛЕуЮЊMЃЌЙ§зјБъдЕуOЕФжБЯпlгыC2ЯрНЛгкЕуAЁЂBЃЌжБЯпMAЃЌMBЗжБ№гыC1ЯрНЛгкЕуDЁЂEЃЎЗжЮі ЃЈIЃЉРыаФТЪ$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$ЃЌПЩЕУa2=2c2=2b2ЃЌгжxжсБЛЧњЯпC2ЃКy=x2-bНиЕУЕФЯпЖЮГЄ2$\sqrt{b}$=2bЃЌНтЕУbЃЌa2ЃЎПЩЕУЧњЯпC2ЕФЗНГЬЃЛЧњЯпC1ЕФЗНГЬЃЎ
ЃЈIIЃЉЩшжБЯпABЕФЗНГЬЮЊЃКy=kxЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎMЃЈ0ЃЌ-1ЃЉЃЎгыХзЮяЯпЗНГЬСЊСЂПЩЕУЃКx2-kx-1=0ЃЌРћгУИљгыЯЕЪ§ЕФЙиЯЕЁЂЪ§СПЛ§дЫЫуаджЪМДПЩжЄУїMAЁЭMBЃЎ
ЃЈIIIЃЉЩшжБЯпMAЕФЗНГЬЃКy=k1x-1ЃЛMBЕФЗНГЬЮЊЃКy=k2x-1ЃЌЧвk1k2=-1ЃЎЗжБ№гыХзЮяЯпЭждВЗНГЬСЊСЂНтЕУAЃЌBЃЌDЃЌEЕФзјБъЃЌРћгУШ§НЧаЮУцЛ§МЦЫуЙЋЪНМДПЩЕУГіЃЌ$\frac{{S}_{1}}{{S}_{2}}$=ІЫЃЌдйРћгУЛљБОВЛЕШЪНЕФаджЪМДПЩЕУГіЃЎ
НтД№ ЃЈIЃЉНтЃКРыаФТЪ$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$ЃЌЁрa2=2c2=2b2ЃЌ
гжxжсБЛЧњЯпC2ЃКy=x2-bНиЕУЕФЯпЖЮГЄ2$\sqrt{b}$=2bЃЌНтЕУb=1ЃЎЁрa2=2ЃЎ
ЁрЧњЯпC2ЕФЗНГЬЮЊЃКy=x2-1ЃЛ
ЧњЯпC1ЕФЗНГЬЮЊЃК$\frac{{x}^{2}}{2}+{y}^{2}$=1ЃЎ
ЃЈIIЃЉжЄУїЃКЩшжБЯпABЕФЗНГЬЮЊЃКy=kxЃЌAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЎMЃЈ0ЃЌ-1ЃЉЃЎ
СЊСЂ$\left\{\begin{array}{l}{y=kx}\\{y={x}^{2}-1}\end{array}\right.$ЃЌЛЏЮЊЃКx2-kx-1=0ЃЌЁрx1+x2=kЃЌx1•x2=-1ЃЎ
Ёр$\overrightarrow{MA}•\overrightarrow{MB}$=x1x2+ЃЈy1+1ЃЉЃЈy2+1ЃЉ=ЃЈk2+1ЃЉx1•x2+kЃЈx1+x2ЃЉ+1=-ЃЈk2+1ЃЉ+k•k+1=0ЃЎ
ЁрMAЁЭMBЃЎ
ЃЈIIIЃЉНтЃКЩшжБЯпMAЕФЗНГЬЃКy=k1x-1ЃЛMBЕФЗНГЬЮЊЃКy=k2x-1ЃЌЧвk1k2=-1ЃЎ
СЊСЂ$\left\{\begin{array}{l}{y={k}_{1}x-1}\\{y={x}^{2}-1}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ЃЌЛђ$\left\{\begin{array}{l}{x={k}_{1}}\\{y={k}_{1}^{2}-1}\end{array}\right.$ЃЌЁрA$ЃЈ{k}_{1}ЃЌ{k}_{1}^{2}-1ЃЉ$ЃЎ
ЭЌРэПЩЕУB$ЃЈ{k}_{2}ЃЌ{k}_{2}^{2}-1ЃЉ$ЃЎ
S1=$\frac{1}{2}$|MA|•|MB|=$\frac{1}{2}$$\sqrt{1+{k}_{1}^{2}}$$\sqrt{1+{k}_{2}^{2}}$|k1|•|k2|ЃЎ
$\left\{\begin{array}{l}{y={k}_{1}x-1}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ЃЌЛђ$\left\{\begin{array}{l}{x=\frac{4{k}_{1}}{1+2{k}_{1}^{2}}}\\{y=\frac{2{k}_{1}^{2}-1}{1+2{k}_{1}^{2}}}\end{array}\right.$ЃЌЁрD$ЃЈ\frac{4{k}_{1}}{1+2{k}_{1}^{2}}ЃЌ\frac{2{k}_{1}^{2}-1}{1+2{k}_{1}^{2}}ЃЉ$ЃЎ
ЭЌРэПЩЕУЃКE$ЃЈ\frac{4{k}_{2}}{1+2{k}_{2}^{2}}ЃЌ\frac{2{k}_{2}^{2}-1}{1+2{k}_{2}^{2}}ЃЉ$ЃЌ
ЁрS2=$\frac{1}{2}|MD|•|ME|$=$\frac{1}{2}$$\sqrt{1+{k}_{1}^{2}}$$\sqrt{1+{k}_{2}^{2}}$•$\frac{|16{k}_{1}{k}_{2}|}{ЃЈ1+2{k}_{1}^{2}ЃЉЃЈ1+2{k}_{2}^{2}ЃЉ}$ЃЎ
Ёр$\frac{{S}_{1}}{{S}_{2}}$=ІЫ=$\frac{ЃЈ1+2{k}_{1}^{2}ЃЉЃЈ1+2{k}_{2}^{2}ЃЉ}{16}$=$\frac{5+2ЃЈ{k}_{1}^{2}+\frac{1}{{k}_{1}^{2}}ЃЉ}{16}$$Ён\frac{9}{16}$ЃЌ
ЫљвдІЫЕФзюаЁжЕЮЊ$\frac{9}{16}$ЃЌДЫЪБk=1Лђ-1ЃЎ
ЕуЦР БОЬтПМВщСЫЭждВгыХзЮяЯпЕФБъзМЗНГЬМАЦфаджЪЁЂжБЯпгыЭждВХзЮяЯпЯрНЛЮЪЬтЁЂШ§НЧаЮУцЛ§МЦЫуЙЋЪНЁЂЛљБОВЛЕШЪНЕФаджЪЁЂЯрЛЅДЙжБЕФжБЯпаБТЪжЎМфЕФЙиЯЕЃЌПМВщСЫЭЦРэФмСІгыМЦЫуФмСІЃЌЪєгкФбЬтЃЎ


 аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
аЁбЇЩњ10ЗжжгПкЫуВтЪд100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{Іа}{6}$ | BЃЎ | $\frac{Іа}{4}$ | CЃЎ | $\frac{Іа}{3}$ | DЃЎ | $\frac{Іа}{2}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | fЁфЃЈ2ЃЉЃМ0 | BЃЎ | fЁфЃЈ2ЃЉ=0 | CЃЎ | fЁфЃЈ2ЃЉЃО0 | DЃЎ | fЁфЃЈ2ЃЉВЛДцдк |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2 | BЃЎ | 1 | CЃЎ | $\frac{1}{4}$ | DЃЎ | $\frac{1}{2}$ |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com