
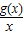 .
.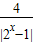 -3)=0有三个相异的实数根,求实数t的取值范围.
-3)=0有三个相异的实数根,求实数t的取值范围.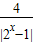 -3)=0,可得|2x-1|+
-3)=0,可得|2x-1|+ +
+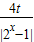 -3t-2=0,利用换元法u=|2x-1|>0,转化为u2-(3t+2)u+(4t+1)=0,当0<u1<1<u2时,原方程有三个相异实根,故可求实数t的取值范围.
-3t-2=0,利用换元法u=|2x-1|>0,转化为u2-(3t+2)u+(4t+1)=0,当0<u1<1<u2时,原方程有三个相异实根,故可求实数t的取值范围.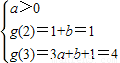 得
得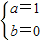
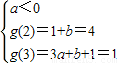 得
得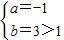 (舍去)
(舍去) …(5分)
…(5分) …(9分)
…(9分)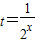 ,∴
,∴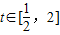 ,∴k≤(t-1)2
,∴k≤(t-1)2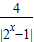 -3)=0,即|2x-1|+
-3)=0,即|2x-1|+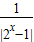 +
+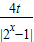 -3t-2=0.
-3t-2=0.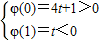 或
或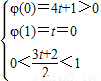 .…(16分)
.…(16分)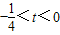 时满足题设.…(18分)
时满足题设.…(18分)

科目:高中数学 来源: 题型:
|
| g(x) |
| x |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| g(x) |
| x |
| 4 |
| |2x-1| |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市张家港市梁丰高级中学高三(上)周日数学试卷(5)(解析版) 题型:解答题
 .
. -3)=0有三个相异的实数根,求实数t的取值范围.
-3)=0有三个相异的实数根,求实数t的取值范围.查看答案和解析>>
科目:高中数学 来源:2012年上海市虹口区高考数学二模试卷(文科)(解析版) 题型:解答题
 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数 .
. 时恒成立,求实数k的取值范围.
时恒成立,求实数k的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com