
已知平面上的线段及点 ,在上任取一点
,在上任取一点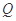 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 到线段的距离,记作
到线段的距离,记作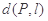 .设是
.设是 长为2的线段,点集
长为2的线段,点集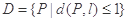 所表示图形的面积为
所表示图形的面积为
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2011年上海市普通高中招生考试理科数学 题型:解答题
(18分)已知平面上的线段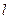 及点
及点 ,在
,在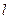 上任取一点
上任取一点 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 到线段
到线段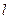 的距离,记作
的距离,记作 。
。
⑴ 求点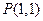 到线段
到线段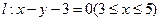 的距离
的距离 ;
;
⑵ 设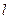 是长为2的线段,求点集
是长为2的线段,求点集 所表示图形的面积;
所表示图形的面积;
⑶ 写出到两条线段 距离相等的点的集合
距离相等的点的集合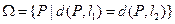 ,其中
,其中 ,
,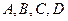 是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
①  。
。
② 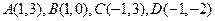 。
。
③  。
。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建泉州五中、莆田、漳州一中高三上期末理数学卷(解析版) 题型:填空题
已知平面上的线段 及点
及点 ,在
,在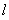 上任取一点
上任取一点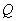 ,线段
,线段 长度的最小值称为点
长度的最小值称为点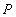 到线段
到线段 的距离,记作
的距离,记作 .设
.设 是长为2的线段,点集
是长为2的线段,点集 所表示图形的面积为________.
所表示图形的面积为________.
查看答案和解析>>
科目:高中数学 来源:2014届江苏省启东市高三上学期第一次检测理科数学试卷(解析版) 题型:填空题
已知平面上的线段 及点
及点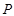 ,任取
,任取 上的一点
上的一点 ,线段
,线段 长度的最小值称为点
长度的最小值称为点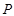 到线段
到线段 的距离,记为
的距离,记为 .设
.设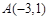 ,
, ,
, ,
,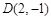 ,
,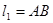 ,
, ,若
,若 满足
满足 ,则
,则 关于
关于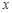 的函数解析式为 .
的函数解析式为 .
查看答案和解析>>
科目:高中数学 来源:2011年上海市招生考试理科数学 题型:解答题
(18分)已知平面上的线段 及点
及点 ,在
,在 上任取一点
上任取一点 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 到线段
到线段 的距离,记作
的距离,记作 。
。
⑴ 求点 到线段
到线段 的距离
的距离 ;
;
⑵ 设 是长为2的线段,求点集
是长为2的线段,求点集 所表示图形的面积;
所表示图形的面积;
⑶ 写出到两条线段 距离相等的点的集合
距离相等的点的集合 ,其中
,其中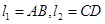 ,
,
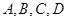 是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
①  。
。
②  。
。
③ 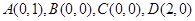 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com