
 �������ߡ���һ�ַ��������Ч�Ķ�����ʽ������ʦÿ���֡������ߡ������üƲ�������ͳ�ƣ������8�조�����ߡ�����������ͳ��ͼ����Ӧ�������������ݱ������
�������ߡ���һ�ַ��������Ч�Ķ�����ʽ������ʦÿ���֡������ߡ������üƲ�������ͳ�ƣ������8�조�����ߡ�����������ͳ��ͼ����Ӧ�������������ݱ������| ������ǧ���� | 16 | 17 | 18 | 19 |
| ������������·� | 400 | 440 | 480 | 520 |
���� ��1��������ͳ��ͼ��֪���ݣ�����������ߡ�������ƽ������
��2��X�ĸ���ȡֵ����Ϊ800��840��880��920���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��У�
��� �⣺��1��������ͳ��ͼ��֪������ʦ��8�조�����ߡ�������ƽ����Ϊ��$\frac{16��3+17��2+18��1+19��2}{8}=17.25$��ǧ������
��2��X�����п���ȡֵΪ��800��840��880��920.$P��X=800��=\frac{C_3^2}{C_6^2}=\frac{1}{5}$��$P��X=840��=\frac{C_3^1C_2^1}{C_6^2}=\frac{2}{5}$��$P��X=880��=\frac{C_3^1C_1^1+C_2^2}{C_6^2}=\frac{4}{15}$��$P��X=880��=\frac{C_2^1C_1^1}{C_6^2}=\frac{2}{15}$��
��X�ķֲ���Ϊ��
| X | 800 | 840 | 880 | 920 |
| P | $\frac{1}{5}$ | $\frac{2}{5}$ | $\frac{4}{15}$ | $\frac{2}{15}$ |
���� ���⿼��ƽ��������������ɢ����������ķֲ��е������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {an}�ǵȲ�������$\left\{{\frac{a_n}{n}}\right\}$���� | |
| B�� | Sn�ǵȲ�����{an}��ǰn��ͣ���$\left\{{\frac{S_n}{n}}\right\}$���� | |
| C�� | {an}�ǵȱ����У�����Ϊq��1 | |
| D�� | �ȱ�����{an}������Ϊ0��q��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{3}{5}$ | B�� | -$\frac{4}{5}$ | C�� | -$\frac{3}{5}$i | D�� | -$\frac{4}{5}$i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
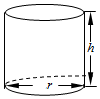 ij�������㽨����ͼ��ʾ��Բ�������������ƺ�ȣ����ȵ�λ���ף����������Ҫ�������ĵ���뾶Ϊr����Ϊh�����Ϊ16�������ף���h��2r����֪Բ���IJ��沿��ÿƽ���������Ϊ3ǧԪ��Բ�����ϡ��µ��沿��ÿƽ���������ΪaǧԪ������������Ľ�����ý����������йأ��������Ľ����ܷ���ΪyǧԪ��
ij�������㽨����ͼ��ʾ��Բ�������������ƺ�ȣ����ȵ�λ���ף����������Ҫ�������ĵ���뾶Ϊr����Ϊh�����Ϊ16�������ף���h��2r����֪Բ���IJ��沿��ÿƽ���������Ϊ3ǧԪ��Բ�����ϡ��µ��沿��ÿƽ���������ΪaǧԪ������������Ľ�����ý����������йأ��������Ľ����ܷ���ΪyǧԪ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | sin����0 | B�� | cos����0 | C�� | sin��cos����0 | D�� | sin��-cos����0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
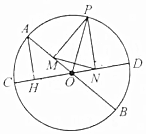 ��ͼ��AB��CD�ǡ�O������ֱ����P��Բ������һ�㣬��PM��AB��PN��CD��AH��CD����֤��MN=AH��
��ͼ��AB��CD�ǡ�O������ֱ����P��Բ������һ�㣬��PM��AB��PN��CD��AH��CD����֤��MN=AH���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com