
【题目】(2015·湖北)一种作图工具如图1所示.O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且![]() ,
,![]() .当栓子D在滑槽AB内作往复运动时,带动N绕O转动一周(D不动时,N也不动),M处的笔尖画出的曲线记为C.以O为原点,AB所在的直线为
.当栓子D在滑槽AB内作往复运动时,带动N绕O转动一周(D不动时,N也不动),M处的笔尖画出的曲线记为C.以O为原点,AB所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(1)求曲线C的方程;
(2)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与曲线C有且只有一个公共点,试探究:
总与曲线C有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
【答案】
(1)
曲线C的方程为![]() 。
。
(2)
![]() 的最小值为8.
的最小值为8.
【解析】1.
设点![]() ,
,![]() 依题意,
依题意,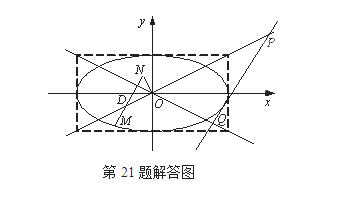
![]() ,且
,且![]() 所以
所以![]() ,且
,且 ,即
,即![]() 且
且![]() .由于当点D不动时,点N也不动,所以t不恒等于0,于是
.由于当点D不动时,点N也不动,所以t不恒等于0,于是![]() ,故
,故![]() ,代入
,代入![]() ,可得
,可得![]() ,即所求的曲线C的方程为
,即所求的曲线C的方程为![]() 。
。
2.
(1)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 为
为![]() 或
或![]() ,都有
,都有![]() .
.
(2)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() ,由
,由![]() 消去
消去![]() ,可得
,可得![]() .因为直线
.因为直线![]() 总与椭圆C有且只有一个公共点,所以
总与椭圆C有且只有一个公共点,所以![]() ,即
,即![]() . ①又由
. ①又由![]() 可得
可得![]() ;同理可得
;同理可得![]() .由原点O到直线
.由原点O到直线![]() 的距离为
的距离为![]() 和
和![]() ,可得
,可得![]() .② 将①代入②得
.② 将①代入②得![]() 。当
。当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .因
.因![]() ,则
,则 ![]() ,
,![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时取等号,所以当
时取等号,所以当![]() 时,
时,![]() 的最小值为8.
的最小值为8.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


科目:高中数学 来源: 题型:
【题目】(2015·四川)已知函数f(x)=2x , g(x)=x2+ax(其中a![]() R).对于不相等的实数x1, x2 , 设m=
R).对于不相等的实数x1, x2 , 设m=![]() ,n=
,n=![]() .
.
现有如下命题:
(1)对于任意不相等的实数x1, x2 , 都有m>0;
(2)对于任意的a及任意不相等的实数x1, x2 , ,都有n>0;
(3)对于任意的a , 存在不相等的实数x1, x2 , 使得m=n;
(4)对于任意的a , 存在不相等的实数x1, x2 , 使得m=-n.
其中的真命题有 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球A1, A2和1个白球B的甲箱与装有2个红球a1,a2和2个白球b1,b2的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(1)用球的标号列出所有可能的摸出结果;
(2)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)设![]() . 若p:
. 若p:![]() 成等比数列;
成等比数列;
q:![]() ,则( )
,则( )
A.p是q的充分条件,但不是q的必要条件
B.p是q的必要条件,但不是q的充分条件
C.p是q的充分必要条件
D.p既不是q的充分条件,也不是q的必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域内的每一个值
对定义域内的每一个值![]() 在其定义域内都存在唯一的
在其定义域内都存在唯一的![]() 使
使![]() 成立,则称该函数为“依赖函数”.
成立,则称该函数为“依赖函数”.
(1)判断函数![]() 是否为“依赖函数”,并说明理由;
是否为“依赖函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上为“依赖函数”,求实数
上为“依赖函数”,求实数![]() 乘积
乘积![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“依赖函数”,若存在实数
上为“依赖函数”,若存在实数![]() 使得对任意的
使得对任意的![]() 有不等式
有不等式![]() 都成立,求实数
都成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() , 点
, 点![]() 在椭圆上且位于第一象限,直线
在椭圆上且位于第一象限,直线![]() 被圆
被圆![]() 截得的线段的长为
截得的线段的长为![]() .(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于
.(1)求直线 F M 的斜率(2)求椭圆的方程(3)设动点 P 在椭圆上,若直线FP的斜率大于![]() ,求直线OP( O 为原点)的斜率的取值范围
,求直线OP( O 为原点)的斜率的取值范围
(1)求直线![]() 的斜率
的斜率
(2)求椭圆的方程
(3)设动点![]() 在椭圆上,若直线
在椭圆上,若直线![]() 的斜率大于
的斜率大于![]() , 求直线
, 求直线![]() (
(![]() 为原点)的斜率的取值范围
为原点)的斜率的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,若将运动员按成绩由好到差编为![]() 号,再用系统抽样方法从中抽取7人,则其中成绩在区间
号,再用系统抽样方法从中抽取7人,则其中成绩在区间![]() 上的运动员人数是
上的运动员人数是 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com