
【题目】把正整数排成如图(a)的三角形阵,然后擦去第偶数行中的所有奇数,第奇数行中的所有偶数,可得如图(b)三角形阵,现将图(b)中的正整数按从小到大的顺序构成一个数列{an},若ak=2017,则k= . 
【答案】1031
【解析】解:由题意,图a中第n行有2n﹣1个数,
前n行有n× ![]() =n×n=n2个数,
=n×n=n2个数,
图b知各行数字个数等于行数,故前n行共有n× ![]() =
= ![]() ,
,
∵图a每行的最后一个数恰好是行号的平方,45×45=2025,
故2017是第45行倒数第9个数,
由图b知各行数字个数等于行数,故前45行共有45× ![]() =1035,
=1035,
由于最后一个数是奇数,
按图b规则知,2017是第45行倒数第5个数,故k=1035﹣4=1031,
所以答案是:1031.
【考点精析】解答此题的关键在于理解归纳推理的相关知识,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 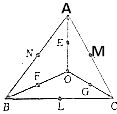
(1)试用 ![]() ,
, ![]() ,
, ![]() 表示向量
表示向量 ![]() ,
, ![]() ,
, ![]() ;
;
(2)证明:线段EL,FM,GN交于一点且互相平分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明计划在8月11日至8月20日期间游览某主题公园,根据旅游局统计数据,该主題公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比, ![]() 以下为舒适,
以下为舒适, ![]() 为一般,
为一般, ![]() 以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览
以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览![]() 天.
天.
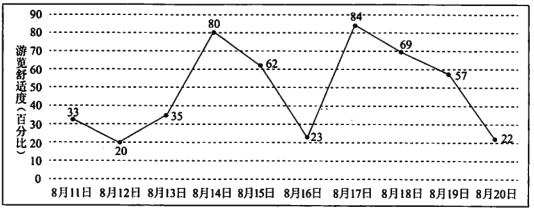
(1)求小明连续两天都遇上拥挤的概率;
(2)设![]() 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() 平面
平面![]() .
.
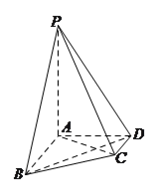
(1)设平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求证: ![]() .
.
(3)设点![]() 为线段
为线段![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn满足:Sn=n2 , 等比数列{bn}满足:b2=2,b5=16
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内的动点P到定直线l:x=![]() 的距离与点P到定点F(
的距离与点P到定点F(![]() ,0)之比为
,0)之比为![]() .
.
(1)求动点P的轨迹C的方程;
(2)若点N为轨迹C上任意一点(不在x轴上),过原点O作直线AB,交(1)中轨迹C于点A、B,且直线AN、BN的斜率都存在,分别为k1、k2,问k1·k2是否为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心在
的圆心在![]() 轴上,并且过
轴上,并且过![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com