考点:函数奇偶性的性质,函数单调性的判断与证明,对数函数的图像与性质
专题:函数的性质及应用
分析:(1)由奇函数可得f(0)=0,可得m值,再由f(1)=-1可得a值;
(2)任取x
1,x
2∈(-2,2),且x
1<x
2,由对数的运算和不等式的放缩法可得作差f(x
1)-f(x
2)>0,可得结论;
(3)不等式可化为f(
)<f(1),由单调性可得1<
<2,易解得答案.
解答:
解:(1)∵f(x)为奇函数,∴f(0)=log
am=0,
解得m=1,∴f(x)=log
a,
又f(1)=-1,∴log
a=-1,解得a=3;
(2)易得函数f(x)=log
3的定义域为(-2,2),
任取x
1,x
2∈(-2,2),且x
1<x
2,
则f(x
1)-f(x
2)=log
3-log
3=log
3>log
3=log
31=0,
∴函数f(x)在(-2,2)单调递减;
(3)不等式f(
)+1<0可化为f(
)<-1,
可化为f(
)<f(1),
由(2)知函数f(x)在(-2,2)单调递减,
∴1<
<2,解得-1<x<0,
∴不等式f(
)+1<0的解集为{x|-1<x<0}.
点评:本题考查函数的奇偶性和单调性,涉及定义法判函数的单调性和单调性的应用,属中档题.



 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案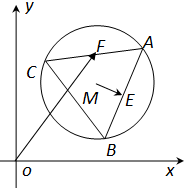 如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,
如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点, 一个社会调查机构就某地居民的月收入调查了10000人,并根所得数据画了样本的频率分布直方图(如图所示)为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在(2500,3000元/月)收入段应抽出( )人.
一个社会调查机构就某地居民的月收入调查了10000人,并根所得数据画了样本的频率分布直方图(如图所示)为了进一步分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在(2500,3000元/月)收入段应抽出( )人.