
【题目】经济订货批量模型,是目前大多数工厂、企业等最常采用的订货方式,即某种物资在单位时间的需求量为某常数,经过某段时间后,存储量消耗下降到零,此时开始订货并随即到货,然后开始下一个存储周期,该模型适用于整批间隔进货、不允许缺货的存储问题,具体如下:年存储成本费![]() (元)关于每次订货
(元)关于每次订货![]() (单位)的函数关系
(单位)的函数关系![]() ,其中
,其中![]() 为年需求量,
为年需求量,![]() 为每单位物资的年存储费,
为每单位物资的年存储费,![]() 为每次订货费. 某化工厂需用甲醇作为原料,年需求量为6000吨,每吨存储费为120元/年,每次订货费为2500元.
为每次订货费. 某化工厂需用甲醇作为原料,年需求量为6000吨,每吨存储费为120元/年,每次订货费为2500元.
(1)若该化工厂每次订购300吨甲醇,求年存储成本费;
(2)每次需订购多少吨甲醇,可使该化工厂年存储成本费最少?最少费用为多少?
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=4y的焦点为F,直线:y=kx+b(k≠0)交抛物线C于A、B两点,|AF|+|BF|=4,M(0,3).
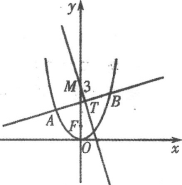
(1)若AB的中点为T,直线MT的斜率为![]() ,证明:k·
,证明:k·![]() 为定值;
为定值;
(2)求△ABM面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F.

(1)求证:EF∥平面PAB;
(2)若PB与平面ABCD所成角的正弦值为![]() ,求二面角P-AE-B的余弦值.
,求二面角P-AE-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 离心率等于
离心率等于![]() ,
,![]() 、
、![]() 是椭圆上的两点.
是椭圆上的两点.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.当
两侧的动点.当![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值?如果为定值,请求出此定值;如果不是定值,请说明理由.
的斜率是否为定值?如果为定值,请求出此定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上动点P到定点![]() 的距离比P到直线
的距离比P到直线![]() 的距离大1.记动点P的轨迹为曲线C.
的距离大1.记动点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点![]() 的直线
的直线![]() 交曲线C于A、B两点,点A关于x轴的对称点是D,证明:直线
交曲线C于A、B两点,点A关于x轴的对称点是D,证明:直线![]() 恒过点F.
恒过点F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com