
ЁОЬтФПЁПЯТСаХаЖЯЃК
ЂйДгИіЬхБрКХЮЊ1ЃЌ2ЃЌЁЃЌ1000ЕФзмЬхжаГщШЁвЛИіШнСПЮЊ50ЕФбљБОЃЌШєВЩгУЯЕЭГГщбљЗНЗЈНјааГщШЁЃЌдђЗжЖЮМфИєгІЮЊ20ЃЛ
ЂквбжЊФГжжВЪЦБЕФжаНБИХТЪЮЊ ![]() ЃЌФЧУДТђ1000еХетжжВЪЦБОЭвЛЖЈЛсжаНБЃЈМйЩшИУВЪЦБгазуЙЛЕФеХЪ§ЃЉЃЛ
ЃЌФЧУДТђ1000еХетжжВЪЦБОЭвЛЖЈЛсжаНБЃЈМйЩшИУВЪЦБгазуЙЛЕФеХЪ§ЃЉЃЛ
ЂлДгзАга2ИіКьЧђКЭ2Иіќ\ЧђЕФПкДќФкШЮШЁ2ИіЧђЃЌЧЁга1Иіќ\ЧђгыЧЁга2Иіќ\ЧђЪЧЛЅГтЕЋВЛЖдСЂЕФСНИіЪТМўЃЛ
ЂмЩшОпгаЯпадЯрЙиЙиЯЕЕФБфСПЕФвЛзщЪ§ОнЪЧЃЈ1ЃЌ3ЃЉЃЌЃЈ2ЃЌ5ЃЉЃЌЃЈ3ЃЌ6ЃЉЃЌЃЈ6ЃЌ8ЃЉЃЌдђЫќУЧЕФЛиЙщжБЯпвЛЖЈЙ§ЕуЃЈ3ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
Цфжае§ШЗЕФађКХЪЧЃЈ ЃЉ
A.ЂйЁЂЂкЁЂЂл
B.ЂйЁЂЂлЁЂЂм
C.ЂлЁЂЂм
D.ЂйЁЂЂл
ЁОД№АИЁПB
ЁОНтЮіЁПНтЃКЂйДгИіЬхБрКХЮЊ1ЃЌ2ЃЌЁЃЌ1000ЕФзмЬхжаГщШЁвЛИіШнСПЮЊ50ЕФбљБОЃЌШєВЩгУЯЕЭГГщбљЗНЗЈНјааГщШЁЃЌдђЗжЖЮМфИєгІЮЊ ![]() =20ЃЌе§ШЗЃЛ
=20ЃЌе§ШЗЃЛ
ЂквбжЊФГжжВЪЦБЕФжаНБИХТЪЮЊ ![]() ЃЌФЧУДТђ1000еХетжжВЪЦБПЩФмЛсжаНБЃЈМйЩшИУВЪЦБгазуЙЛЕФеХЪ§ЃЉЃЌВЛе§ШЗЃЛ
ЃЌФЧУДТђ1000еХетжжВЪЦБПЩФмЛсжаНБЃЈМйЩшИУВЪЦБгазуЙЛЕФеХЪ§ЃЉЃЌВЛе§ШЗЃЛ
ЂлДгзАга2ИіКьЧђКЭ2Иіќ\ЧђЕФПкДќФкШЮШЁ2ИіЧђЃЌШЁЗЈЧщПіАќРЈЃК2ИіЖМЪЧКьЧђЃЛ2ИіЖМЪЧКкЧђЃЛ1ИіКьЧђЃЌ1ИіКкЧђШ§РрЃЎЧЁга1Иіќ\ЧђгыЧЁга2Иіќ\ЧђЛЅГтВЛЖдСЂЃЌе§ШЗЃЛ
ЂмЩшОпгаЯпадЯрЙиЙиЯЕЕФБфСПЕФвЛзщЪ§ОнЪЧЃЈ1ЃЌ3ЃЉЃЌЃЈ2ЃЌ5ЃЉЃЌЃЈ3ЃЌ6ЃЉЃЌЃЈ6ЃЌ8ЃЉЃЌдђЫќУЧЕФЛиЙщжБЯпвЛЖЈЙ§ЕуЃЈ3ЃЌ ![]() ЃЉЃЌе§ШЗЃЎ
ЃЉЃЌе§ШЗЃЎ
ЙЪбЁЃКBЃЎ
Жд4ИібЁЯюЗжБ№НјааХаЖЯЃЌМДПЩЕУГіНсТлЃЎ


 жЧШЄЪюМйЮТЙЪжЊаТЯЕСаД№АИ
жЧШЄЪюМйЮТЙЪжЊаТЯЕСаД№АИ гЂгяаЁгЂалЬьЬьФЌаДЯЕСаД№АИ
гЂгяаЁгЂалЬьЬьФЌаДЯЕСаД№АИ ЪюМйзївЕАВЛеЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ
ЪюМйзївЕАВЛеЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁАвЛДјвЛТЗЁБЕФНЈЩшжаЃЌжаЪЏЛЏМЏЭХЛёЕУСЫФГЕиЩюКЃгЭЬяЧјПщЕФПЊВЩШЈЃЌМЏЭХдкИУЕиЧјЫцЛњГѕВНПБЬНСЫМИПкОЎЃЌШЁЕУСЫЕижЪзЪСЯ.НјШыШЋУцПБЬНЪБЦкКѓЃЌМЏЭХАДЭјТчЕуРДВМжУОЎЮЛНјааШЋУцПБЬН.гЩгкПБЬНвЛПкОЎЕФЗбгУКмИпЃЌШчЙћаТЩшМЦЕФОЎЮЛгыдгаОЎЮЛжиКЯЛђНгНќЃЌБуРћгУОЩОЎЕФЕижЪзЪСЯЃЌВЛБиДђетПкаТОЎЃЌвдНкдМПБЬНЗбгУ.ПБЬНГѕЦкЪ§ОнзЪСЯЯТБэЃК
ОЎКХI | 1 | 2 | 3 | 4 | 5 | 6 |
зјБъ |
|
|
|
|
|
|
зъЬНЩюЖШ | 2 | 4 | 5 | 6 | 8 | 10 |
ГігЭСП | 40 | 70 | 110 | 90 | 160 | 205 |
ЃЈ1ЃЉдкЩЂЕуЭМжа![]() КХОЩОЎЮЛжУДѓжТЗжВМдквЛЬѕжБЯпИННќЃЌНшжњЧА5зщЪ§ОнЧѓЕУЛиЙщЯпЗНГЬЮЊ
КХОЩОЎЮЛжУДѓжТЗжВМдквЛЬѕжБЯпИННќЃЌНшжњЧА5зщЪ§ОнЧѓЕУЛиЙщЯпЗНГЬЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЃЌВЂЙРМЦ
ЃЌВЂЙРМЦ![]() ЕФдЄБЈжЕЃЛ
ЕФдЄБЈжЕЃЛ
ЃЈ2ЃЉЯжзМБИПБЬНаТОЎ![]() ЃЌШєЭЈЙ§1ЁЂ3ЁЂ5ЁЂ7КХОЎМЦЫуГіЕФ
ЃЌШєЭЈЙ§1ЁЂ3ЁЂ5ЁЂ7КХОЎМЦЫуГіЕФ![]() ЕФжЕЃЈ
ЕФжЕЃЈ![]() ОЋШЗЕН0.01ЃЉЯрБШгкЃЈ1ЃЉжа
ОЋШЗЕН0.01ЃЉЯрБШгкЃЈ1ЃЉжа![]() ЕФжЕжЎВюЃЈМДЃК
ЕФжЕжЎВюЃЈМДЃК ![]() ЃЉВЛГЌЙ§10%ЃЌдђЪЙгУЮЛжУзюНгНќЕФвбгаОЩОЎ
ЃЉВЛГЌЙ§10%ЃЌдђЪЙгУЮЛжУзюНгНќЕФвбгаОЩОЎ![]() ЃЌЗёдђдкаТЮЛжУДђОЎЃЌЧыХаЖЯПЩЗёЪЙгУОЩОЎЃПЃЈВЮПМЙЋЪНКЭМЦЫуНсЙћЃК
ЃЌЗёдђдкаТЮЛжУДђОЎЃЌЧыХаЖЯПЩЗёЪЙгУОЩОЎЃПЃЈВЮПМЙЋЪНКЭМЦЫуНсЙћЃК 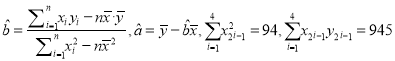 ЃЉ
ЃЉ
ЃЈ3ЃЉЩшГігЭСПгызъЬНЩюЖШЕФБШжЕ![]() ВЛЕЭгк20ЕФПБЬНОЎГЦЮЊгХжЪОЎЃЌдкдгаОЎКХ
ВЛЕЭгк20ЕФПБЬНОЎГЦЮЊгХжЪОЎЃЌдкдгаОЎКХ![]() ЕФОЎжаШЮвтПБЬН3ПкОЎЃЌЧѓЧЁКУ2ПкЪЧгХжЪОЎЕФИХТЪЃЎ
ЕФОЎжаШЮвтПБЬН3ПкОЎЃЌЧѓЧЁКУ2ПкЪЧгХжЪОЎЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯђСП ![]() ЃЌ
ЃЌ ![]() Тњзу|
Тњзу| ![]() |=
|= ![]() ЃЌ|
ЃЌ| ![]() |=1ЃЌЧвЖдШЮвтЪЕЪ§xЃЌВЛЕШЪН|
|=1ЃЌЧвЖдШЮвтЪЕЪ§xЃЌВЛЕШЪН| ![]() +x
+x ![]() |Ён|
|Ён| ![]() +
+ ![]() |КуГЩСЂЃЌЩш
|КуГЩСЂЃЌЩш ![]() гы
гы ![]() ЕФМаНЧЮЊІШЃЌдђtan2ІШ=ЃЈ ЃЉ
ЕФМаНЧЮЊІШЃЌдђtan2ІШ=ЃЈ ЃЉ
A.Љ ![]()
B.![]()
C.Љ ![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ТњзуЃКa1= ![]() ЃЌa2=
ЃЌa2= ![]() ЃЌ2an=an+1+anЉ1ЃЈnЁн2ЃЌnЁЪNЃЉЃЌЪ§Са{bn}ТњзуЃКb1ЃМ0ЃЌ3bnЉbnЉ1=nЃЈnЁн2ЃЌnЁЪRЃЉЃЌЪ§Са{bn}ЕФЧАnЯюКЭЮЊSn ЃЎ
ЃЌ2an=an+1+anЉ1ЃЈnЁн2ЃЌnЁЪNЃЉЃЌЪ§Са{bn}ТњзуЃКb1ЃМ0ЃЌ3bnЉbnЉ1=nЃЈnЁн2ЃЌnЁЪRЃЉЃЌЪ§Са{bn}ЕФЧАnЯюКЭЮЊSn ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЪ§Са{bnЉan}ЮЊЕШБШЪ§СаЃЛ
ЃЈ2ЃЉЧѓжЄЃКЪ§Са{bn}ЮЊЕндіЪ§СаЃЛ
ЃЈ3ЃЉШєЕБЧвНіЕБn=3ЪБЃЌSnШЁЕУзюаЁжЕЃЌЧѓb1ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ ![]() =ЃЈ1ЃЌ0ЃЉЃЌ
=ЃЈ1ЃЌ0ЃЉЃЌ ![]() =ЃЈ2ЃЌ1ЃЉЃЎ
=ЃЈ2ЃЌ1ЃЉЃЎ
ЃЈ1ЃЉЧѓ ![]() +3
+3 ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЕБkЮЊКЮЪЕЪ§ЪБЃЌk ![]() Љ
Љ ![]() гы
гы ![]() +3
+3 ![]() ЦНааЃЌЦНааЪБЫќУЧЪЧЭЌЯђЛЙЪЧЗДЯђЃП
ЦНааЃЌЦНааЪБЫќУЧЪЧЭЌЯђЛЙЪЧЗДЯђЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§Са{an}ЪЧЕШВюЪ§СаЃЌШє ![]() ЃМЉ1ЃЌЧвЫќЕФЧАnЯюКЭSnгазюДѓжЕЃЌФЧУДЕБSnШЁЕФзюаЁе§жЕЪБЃЌn=ЃЈ ЃЉ
ЃМЉ1ЃЌЧвЫќЕФЧАnЯюКЭSnгазюДѓжЕЃЌФЧУДЕБSnШЁЕФзюаЁе§жЕЪБЃЌn=ЃЈ ЃЉ
A.11
B.17
C.19
D.21
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§f(x)=(1-x2)ex.
ЃЈ1ЃЉЬжТлf(x)ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉЕБx![]() 0ЪБЃЌf(x)
0ЪБЃЌf(x)![]() ax+1ЃЌЧѓaЕФШЁжЕЗЖЮЇ.
ax+1ЃЌЧѓaЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§y=fЃЈxЃЉЃЌНЋfЃЈxЃЉЭМЯёбиxжсЯђгвЦНвЦ ![]() ИіЕЅЮЛЃЌШЛКѓАбЫљЕУЕНЭМЯёЩЯУПвЛЕуЕФзнзјБъБЃГжВЛБфЃЌКсзјБъРЉДѓЕНдРДЕФ2БЖЃЌетбљЕУЕНЕФЧњЯпгыy=2sinЃЈxЉ
ИіЕЅЮЛЃЌШЛКѓАбЫљЕУЕНЭМЯёЩЯУПвЛЕуЕФзнзјБъБЃГжВЛБфЃЌКсзјБъРЉДѓЕНдРДЕФ2БЖЃЌетбљЕУЕНЕФЧњЯпгыy=2sinЃЈxЉ ![]() ЃЉЕФЭМЯёЯрЭЌЃЌФЧУДy=fЃЈxЃЉЕФНтЮіЪНЮЊЃЈ ЃЉ
ЃЉЕФЭМЯёЯрЭЌЃЌФЧУДy=fЃЈxЃЉЕФНтЮіЪНЮЊЃЈ ЃЉ
A.fЃЈxЃЉ=2sinЃЈ2xЉ ![]() ЃЉ
ЃЉ
B.fЃЈxЃЉ=2sinЃЈ2xЉ ![]() ЃЉ
ЃЉ
C.fЃЈxЃЉ=2sinЃЈ2x+ ![]() ЃЉ
ЃЉ
D.fЃЈxЃЉ=2sinЃЈ2x+ ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнЬтвтНтД№
ЃЈ1ЃЉвбжЊКЏЪ§fЃЈxЃЉ= ![]() +9xЃЌШєxЃО0ЃЌЧѓfЃЈxЃЉЕФзюаЁжЕМАДЫЪБЕФxжЕЃЎ
+9xЃЌШєxЃО0ЃЌЧѓfЃЈxЃЉЕФзюаЁжЕМАДЫЪБЕФxжЕЃЎ
ЃЈ2ЃЉНтВЛЕШЪНЃЈx+2ЃЉЃЈ3ЉxЃЉЁн0ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com