
| A. | y2=4x | B. | y2=6x | C. | y2=8x | D. | y2=9x |
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
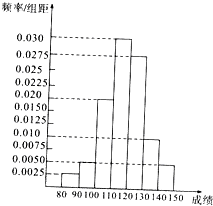 某县有甲乙丙丁四所高中的五千名学生参加了高三的调研测试,为了解数学学科的成绩情况,现从中随机抽取若干名学生在这次测试中的数学成绩作为样本,(其中甲学校抽取了30人),制成如下频率分布表并得到相应的频率分布直方图:
某县有甲乙丙丁四所高中的五千名学生参加了高三的调研测试,为了解数学学科的成绩情况,现从中随机抽取若干名学生在这次测试中的数学成绩作为样本,(其中甲学校抽取了30人),制成如下频率分布表并得到相应的频率分布直方图:| 分组 | 频数 | 频率 |
| [80,90) | 0.025 | |
| [90,100) | 6 | |
| [100,110) | ||
| [110,120) | ||
| [120,130) | ||
| [130,140) | 12 | |
| [140,150) | 0.05 | |
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 9 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
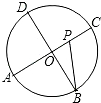 如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线作匀速运动,设运动时间为t(s).∠APB=y(单位:度),则下列图象中表示y与t之间函数关系最恰当的是( )
如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O-C-D-O路线作匀速运动,设运动时间为t(s).∠APB=y(单位:度),则下列图象中表示y与t之间函数关系最恰当的是( )| A. | 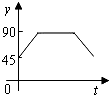 | B. | 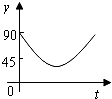 | C. |  | D. | 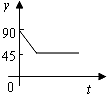 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
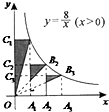 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.
如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{4}}]$ | B. | (0,1) | C. | $[{\frac{1}{4},1})$ | D. | (0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com