
【题目】已知函数f(x)=axlnx﹣x2﹣ax+1(a∈R)在定义域内有两个不同的极值点.
(1)求实数a的取值范围;
(2)设两个极值点分别为x1,x2,x1<x2,证明:f(x1)+f(x2)<2﹣x12+x22.
【答案】(1)a>2e(2)证明见解析
【解析】
(1)先对函数求导,然后结合导数与单调性的关系对a进行分类讨论,确定导数正负即可求解函数单调性,结合单调性即可求解;
(2)分析要证明不等式特点,进行合理的变形,然后构造函数,结合导数及函数性质可证.
(1)由题意可知,f(x)的定义域为(0,+∞),f'(x)=alnx﹣2x,
令g(x)=alnx﹣2x(x>0),
由函数f(x)在定义域内有两个不同的极值点,可知g(x)在区间(0,+∞)内有两个不同的变号零点,
由![]() 可知,
可知,
当a≤0时,g'(x)<0恒成立,即函数g(x)在(0,+∞)上单调,不符合题意,舍去.
当a>0时,由g'(x)>0得,![]() ,即函数g(x)在区间
,即函数g(x)在区间![]() 上单调递增;
上单调递增;
由g'(x)<0得,![]() ,即函数g(x)在区间
,即函数g(x)在区间![]() 上单调递减;
上单调递减;
故要满足题意,必有![]() ,
,
解得:a>2e;
又![]() ,∴函数g(x)在(1,
,∴函数g(x)在(1,![]() )内有一个零点,
)内有一个零点,
又当![]() 时,g(x)
时,g(x)![]() ,∴在(
,∴在(![]() )内有一个零点,
)内有一个零点,
∴a>2e满足题意.
(2)由(1)可知,![]() ,
,
故要证:![]() ,
,
只需证明:![]() ,
,
即证: 不妨设0<x1<x2,即证
不妨设0<x1<x2,即证![]() ,
,
构造函数:h(t)=lnt﹣t2+1(t>1)其中![]() ,
,
由![]() ,所以函数h(t)在区间(1,+∞)内单调递减,所以h(t)<h(1)=0得证.
,所以函数h(t)在区间(1,+∞)内单调递减,所以h(t)<h(1)=0得证.


科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 (t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程及弦AB的长;
(2)动点P在圆C上(不与A,B重合),试求△ABP的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶100户贫困户.工作组对这100户村民的贫困状况和家庭成员受教育情况进行了调查:甲村55户贫困村民中,家庭成员接受过中等及以上教育的只有10户,乙村45户贫困村民中,家庭成员接受过中等及以上教育的有20户.
(1)完成下面的列联表,并判断是否有99.5%的把握认为贫困与接受教育情况有关;
家庭成员接受过中等以下 教育的户数 | 家庭成员接受过中等及以上 教育的户数 | 合计 | |
甲村贫困户数 | |||
乙村贫困户数 | |||
合计 |
(2)在被帮扶的100户贫困户中,按分层抽样的方法从家庭成员接受过中等及以上教育的贫困户中抽取6户,再从这6户中采用简单随机抽样的方法随机抽取2户,求这2户中甲、乙两村恰好各1户的概率.
参考公式与数据: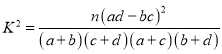 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).


(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高三年级该学科成绩中任意抽取3名学生的成绩,求至少2名学生的成绩为优分的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是由正整数组成的无穷数列.若存在常数
是由正整数组成的无穷数列.若存在常数![]() ,使得
,使得![]() 任意的
任意的![]() 成立,则称数列
成立,则称数列![]() 具有性质
具有性质![]() .
.
(1)分别判断下列数列![]() 是否具有性质
是否具有性质![]() ; (直接写出结论)
; (直接写出结论)
①![]()
②![]()
(2)若数列![]() 满足
满足![]() ,求证:“数列
,求证:“数列![]() 具有性质
具有性质![]() ”是“数列
”是“数列![]() 为常数列”的充分必要条件;
为常数列”的充分必要条件;
(3)已知数列![]() 中
中![]() 且
且![]() .若数列
.若数列![]() 具有性质
具有性质![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近五年来某草场羊只数量与草场植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 | 1 | 2 | 3 | 4 | 5 |
羊只数量(万只) | 1.4 | 0.9 | 0.75 | 0.6 | 0.3 |
草地植被指数 | 1.1 | 4.3 | 15.6 | 31.3 | 49.7 |

根据表及图得到以下判断:①羊只数量与草场植被指数成减函数关系;②若利用这五组数据得到的两变量间的相关系数为![]() ,去掉第一年数据后得到的相关系数为
,去掉第一年数据后得到的相关系数为![]() ,则
,则![]() ;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
;③可以利用回归直线方程,准确地得到当羊只数量为2万只时的草场植被指数;以上判断中正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|2x+2|,g(x)=|x+2|﹣|x﹣2a|+a.
(1)求不等式f(x)>4的解集;
(2)对x1∈R,x2∈R,使得f(x1)≥g(x2)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行元旦促销回馈活动,凡购物满1000元,即可参与抽奖活动,抽奖规则如下:在一个不透明的口袋中装有编号为1、2、3、4、5的5个完全相同的小球,顾客每次从口袋中摸出一个小球,共摸三次(每次摸出的小球均不放回口袋),编号依次作为一个三位数的个位、十位、百位,若三位数是奇数,则奖励50元,若三位数是偶数,则奖励![]() 元(
元(![]() 为三位数的百位上的数字,如三位数为234,则奖励
为三位数的百位上的数字,如三位数为234,则奖励![]() 元).
元).
(1)求抽奖者在一次抽奖中所得三位数是奇数的概率;
(2)求抽奖者在一次抽奖中获奖金额![]() 的概率分布与期望
的概率分布与期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com