
【题目】设过抛物线 ![]() 的焦点
的焦点 ![]() 的直线
的直线 ![]() 交抛物线于点
交抛物线于点 ![]() ,若以
,若以 ![]() 为直径的圆过点
为直径的圆过点 ![]() ,且与
,且与 ![]() 轴交于
轴交于 ![]() ,
, ![]() 两点,则
两点,则 ![]() ( )
( )
A.3
B.2
C.-3
D.-2
【答案】C
【解析】抛物线焦点坐标为F(1,0),准线方程为x=﹣1
设直线MN的方程为x=ty+1,A、B的坐标分别为( ![]() ,y1),(
,y1),( ![]() ,y2)
,y2)
联立直线和抛物线得到方程:y2﹣4my﹣4=0,
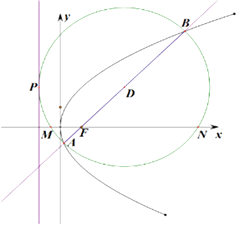
∴y1+y2=4m,y1y2=﹣4,
x1+x2=ty1+1+ty2+1=t(y1+y2)+2=4t2+2, ![]() =2t2+1,
=2t2+1, ![]() =2t,
=2t,
则圆心D(2t2+1,2t),
由抛物线的性质可知:丨AB丨=x1+x2+p=4(t2+1),
由P到圆心的距离d= ![]() ,由题意可知:d=
,由题意可知:d= ![]() 丨AB丨,
丨AB丨,
解得:t=1,则圆心为(3,2),半径为4,∴圆的方程方程为(x﹣3)2+(y﹣2)2=42,
则当y=0,求得与x轴的交点坐标,假设m>n,则m=3﹣2 ![]() ,n=3+2
,n=3+2 ![]() ,
,
∴mn=(3﹣2 ![]() )(3+2
)(3+2 ![]() )=﹣3,
)=﹣3,
所以答案是:C.
【考点精析】掌握圆的标准方程是解答本题的根本,需要知道圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
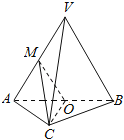
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,则下列结论中正确的是__________.
,则下列结论中正确的是__________.
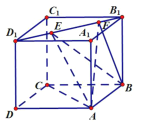
①![]() 平面
平面![]() ;
;
②平面![]() 平面
平面![]() ;
;
③三棱锥![]() 的体积为定值;
的体积为定值;
④存在某个位置使得异面直线![]() 与
与![]() 成角
成角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1曰8日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值![]() 与这种新材料的含量
与这种新材料的含量![]() (单位:克)的关系为:当
(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得数据如表(部分)
.测得数据如表(部分)
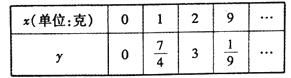
(1)求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(2)其函数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为
是边长为 ![]() 的正方形,
的正方形, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与平面
与平面 ![]() 所成角为
所成角为 ![]() .
.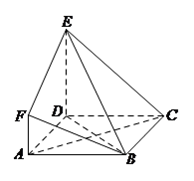
(Ⅰ)求证: ![]() 平面
平面 ![]() .
.
(Ⅱ)求二面角 ![]() 的余弦值.
的余弦值.
(Ⅲ)设点 ![]() 是线段
是线段 ![]() 上一个动点,试确定点
上一个动点,试确定点 ![]() 的位置,使得
的位置,使得 ![]() 平面
平面 ![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos2(ωx+φ)+1(A>0,ω>0)的最大值为3,f(x)的图象在y轴上的截距为2,其相邻两对称轴间的距离为1,则f(1)+f(2)+f(3)+…+f(100)=( )
A.0
B.100
C.150
D.200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx,若存在x1 , x2 , ,xm满足0≤x1<x2<xm≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+|f(xn﹣1)﹣f(xn)|=12,(m≥2,m∈N*),则m的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,它的一个焦点到短轴顶点的距离为2,动直线l:y=kx+m交椭圆E于A、B两点,设直线OA、OB的斜率都存在,且
,它的一个焦点到短轴顶点的距离为2,动直线l:y=kx+m交椭圆E于A、B两点,设直线OA、OB的斜率都存在,且 ![]() .
.
(1)求椭圆E的方程;
(2)求证:2m2=4k2+3;
(3)求|AB|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com