
【题目】曲线![]() 上任意一点M满足
上任意一点M满足![]() , 其中F
, 其中F![]() (-
(-![]() F
F![]() (
(![]() 抛物线
抛物线![]() 的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
(I)求![]() ,
, ![]() 的标准方程;
的标准方程;
(II)请问是否存在直线l满足条件:① 过![]() 的焦点
的焦点![]() ;② 与
;② 与![]() 交于不同两点
交于不同两点![]() ,
, ![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)由已知得曲线![]() 是以
是以![]() 为焦点,以4为实轴的椭圆,抛物线
为焦点,以4为实轴的椭圆,抛物线![]() 的焦点是
的焦点是![]() ,顶点为原点
,顶点为原点![]() ,由此能求出求
,由此能求出求![]() ,
, ![]() 的标准方程;(2)设直线
的标准方程;(2)设直线![]() 的方程为
的方程为![]() ,由
,由 ,得
,得![]() ,由此利用韦达定理结合向量垂直数量积为0的性质能求出直线
,由此利用韦达定理结合向量垂直数量积为0的性质能求出直线![]() 的方程.
的方程.
试题解析:(1)∵曲线![]() 上任意一点
上任意一点![]() 满足
满足![]() ,其中
,其中![]() ,
,
∴曲线![]() 是以
是以![]() 为焦点,以4为实轴的椭圆,
为焦点,以4为实轴的椭圆,
∴![]() ,
, ![]() ,∴
,∴![]() ,∴曲线
,∴曲线![]() 的方程为
的方程为![]() .
.
∵抛物线![]() 的焦点是直线
的焦点是直线![]() 与
与![]() 轴的交点,顶点为原点
轴的交点,顶点为原点![]() ,
,
∴抛物线![]() 的焦点是
的焦点是![]() ,∴抛物线
,∴抛物线![]() 的标准方程为:
的标准方程为: ![]() .
.
(2)假设存在存在直线直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交于不同两点
交于不同两点![]() ,且满足
,且满足![]() ,当直线
,当直线![]() 的斜率
的斜率![]() 不存在时,直线
不存在时,直线![]() 的方程为
的方程为![]() ,不满足条件;
,不满足条件;
当直线![]() 的斜率
的斜率![]() 存在时,设直线
存在时,设直线![]() 的方程为
的方程为![]() ,
,
由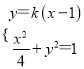 ,得
,得![]() ,设
,设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,∴
,∴ ,
,
解得![]() 或
或![]() ,
,
∴直线![]() 满足条件,且
满足条件,且![]() 的方程为
的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆.
(1) 求实数m的取值范围;
(2) 求该圆半径r的取值范围;
(3) 求该圆心的纵坐标的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
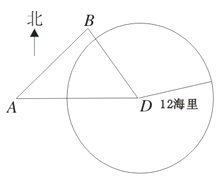
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处。
海里处。
(Ⅰ)求此时该外国船只与![]() 岛的距离;
岛的距离;
(Ⅱ)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方向航行。为了将该船拦截在离
海里的速度沿正南方向航行。为了将该船拦截在离![]() 岛
岛![]() 海里处,不让其进入
海里处,不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值.
海里内的海域,试确定海监船的航向,并求其速度的最小值.
(参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
“健步走”是一种方便而又有效的锻炼方式,李老师每天坚持“健步走”,并用计步器进行统计.他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如下:

(I)求李老师这8天“健步走”步数的平均数;
(II)从步数为16千步,17千步,18千步的6天中任选2天,设李老师这2天通过“健步走”消耗的能量和为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
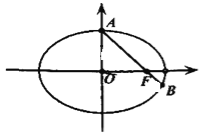
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,短轴长为2,
,短轴长为2,![]() 为原点,直线
为原点,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,且
,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若在椭圆
两点,若在椭圆![]() 上存在点
上存在点![]() ,使
,使![]() 为平行四边形,求
为平行四边形,求![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形ABCD中,AD∥BC,∠ADC=90°,A(-3,-10),
B (-2,-1),C(3,4),
(1)求边AD和CD所在的直线方程;
(2)数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在直线CD上,求证
在直线CD上,求证![]() 为等比数列.
为等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com