
【题目】已知等差数列{an}的前n项和为Sn , 公差d≠0,且S3+S5=50,a1 , a4 , a13成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 ![]() +
+ ![]() +…+
+…+ ![]() =an﹣1(n∈N*),求数列{nbn}的前n项和Tn .
=an﹣1(n∈N*),求数列{nbn}的前n项和Tn .
【答案】
(1)解:依题意得, 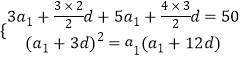
解得 ![]() ,
,
∴an=a1+(n﹣1)d=3+2(n﹣1)=2n+1
(2)解:由(1)得, ![]() ,
,
当n≥2时, ![]() ,
,
两式相减得, ![]() ,则bn=23n(n≥2)
,则bn=23n(n≥2)
当n=1时满足上式,
所以bn=23n(n∈N*),∴nbn=2n3n(n∈N*),
Tn=231+432+633+…+2n3n,
∴3Tn=232+433+634+…+2n3n+1,
两式相减得,﹣2Tn=231+232+233+…+23n﹣2n3n+1
=2(31+32+33+…+3n)﹣2n3n+1
= ![]() ﹣2n3n+1=(1﹣2n)3n+1﹣3
﹣2n3n+1=(1﹣2n)3n+1﹣3
∴Tn= ![]() .
.
【解析】(1)由等差数列的通项公式、前n项和公式,等比中项的性质列出方程组,求出a1、d的值,代入等差数列的通项公式即可求出an;(2)由(1)化简已知的式子,令n取n﹣1代入化简得到另外一个式子,两个式子相减后求出bn , 代入nbn化简,利用错位相减法和等比数列前n项和公式求出Tn .
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系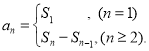 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,圆
,圆![]() ,以动点
,以动点![]() 为圆心的圆经过点
为圆心的圆经过点![]() ,且圆
,且圆![]() 与圆
与圆![]() 内切.
内切.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆的参数方程为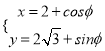 (
(![]() 为参数),以直角坐标系的原点为极点,
为参数),以直角坐标系的原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)将圆的参数方程化为普通方程,再化为极坐标方程;
(Ⅱ)若点![]() 在直线
在直线![]() 上,当点
上,当点![]() 到圆的距离最小时,求点
到圆的距离最小时,求点![]() 的极坐标.
的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣3,3x4﹣2,3x5﹣2的平均数和方差分别为( )
A.2, ![]()
B.4,3
C.4, ![]()
D.2,1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)对任意的x∈R都有f′(x)>f(x)恒成立,则( )
A.3f(ln2)>2f(ln3)
B.3f(ln2)=2f(ln3)
C.3f(ln2)<2f(ln3)
D.3f(ln2)与2f(ln3)的大小不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com