
【题目】某市约有20万住户,为了节约能源,拟出台“阶梯电价”制度,即制定住户月用电量的临界值![]() ,若某住户某月用电量不超过
,若某住户某月用电量不超过![]() 度,则按平价(即原价)0.5(单位:元/度)计费;若某月用电量超过
度,则按平价(即原价)0.5(单位:元/度)计费;若某月用电量超过![]() 度,则超出部分按议价
度,则超出部分按议价![]() (单位:元/度)计费,未超出部分按平价计费.为确定
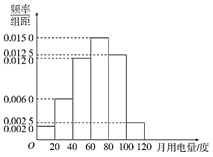
(单位:元/度)计费,未超出部分按平价计费.为确定![]() 的值,随机调查了该市100户的月用电量,统计分析后得到如图所示的频率分布直方图.根据频率分布直方图解答以下问题(同一组数据用该区间的中点值作代表).
的值,随机调查了该市100户的月用电量,统计分析后得到如图所示的频率分布直方图.根据频率分布直方图解答以下问题(同一组数据用该区间的中点值作代表).
(1)若该市计划让全市![]() 的住户在“阶梯电价”出台前后缴纳的电费不变,求临界值
的住户在“阶梯电价”出台前后缴纳的电费不变,求临界值![]() ;
;
(2)在(1)的条件下,假定出台“阶梯电价”之后,月用电量未达![]() 度的住户用电量保持不变;月用电量超过
度的住户用电量保持不变;月用电量超过![]() 度的住户节省“超出部分”的
度的住户节省“超出部分”的![]() ,试估计全市每月节约的电量;
,试估计全市每月节约的电量;
(3)在(1)(2)条件下,若出台“阶梯电价”前后全市缴纳电费总额不变,求议价![]() .
.
【答案】(1)80;(2)![]() 度;(3)
度;(3)![]()
【解析】
(1)计算出每组的频率,找出满足题意的分组后样本估计总体即可得解;
(2)由题意计算出样本中100户住户每月共节电度数,乘以![]() 后即可得解;
后即可得解;
(3)由题意,仅对样本中“超出部分”对应的总电费进行考虑即可:“超出部分”由![]() 度变为
度变为![]() 度,计算即可得解.
度,计算即可得解.
(1)由频率分布直方图,可算得各组数据对应的频率及频数,如表:
分组 |
|
|
|
|
|
|
频率 | 0.04 | 0.12 | 0.24 | 0.30 | 0.25 | 0.05 |
频数 | 4 | 12 | 24 | 30 | 25 | 5 |
由表可知,区间![]() 内的频率总和恰为0.7,由样本估计总体,可得临界值
内的频率总和恰为0.7,由样本估计总体,可得临界值![]() 的值为80.
的值为80.
(2)由(1)知,月用电量在![]() 内的70户住户在“阶梯电价”出台前后用电量不变,节电量为0度;
内的70户住户在“阶梯电价”出台前后用电量不变,节电量为0度;
月用电量在![]() 内的25户住户,平均每户用电90度,超出部分为10度,根据题意,每户每月节电
内的25户住户,平均每户用电90度,超出部分为10度,根据题意,每户每月节电![]() 度,25户每月共节电
度,25户每月共节电![]() (度);
(度);
月用电量在![]() 内的5户住户,平均每户用电110度,超出部分为30度,根据题意,每户每月节电
内的5户住户,平均每户用电110度,超出部分为30度,根据题意,每户每月节电![]() (度),5户每月共节电
(度),5户每月共节电![]() (度).
(度).
故样本中100户住户每月共节电![]() (度),
(度),
用样本估计总体,得全市每月节电量约为![]() (度).
(度).
(3)由题意,全市缴纳电费总额不变,由于“未超出部分”的用电量在“阶梯电价”前后不发生改变,故“超出部分”对应的总电费也不变,由(1)(2)可知,在100户住户组成的样本中,每月用电量的“超出部分”共计![]() (度),实行“阶梯电价”之后,“超出部分”节约了240度,剩余160度,因为“阶梯电价”前后电费总额不变,所以
(度),实行“阶梯电价”之后,“超出部分”节约了240度,剩余160度,因为“阶梯电价”前后电费总额不变,所以![]() ,解得
,解得![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为 ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与曲线
与曲线![]() 两交点所在直线的极坐标方程;
两交点所在直线的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x-![]() (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(1)若对[1,+![]() )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=l时,求最大的正整数k,使得对[e,3](e=2.71828是自然对数的底数)内的任意k个实数x1,x2,,xk都有![]() 成立;
成立;
(3)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( ).
①在![]() 中,若
中,若![]() ,则
,则![]() 是等腰三角形;
是等腰三角形;
②在![]() 中,若
中,若 ![]() ,则
,则![]()
③两个向量![]() ,
,![]() 共线的充要条件是存在实数
共线的充要条件是存在实数![]() ,使
,使![]()
④等差数列的前![]() 项和公式是常数项为0的二次函数.
项和公式是常数项为0的二次函数.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图判断闰年的流程图,判断公元1900年、公元2000年、公元2018年、公元2020年这四年中闰年的个数为(nMODm为n除以m的余数)( )
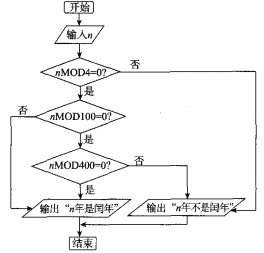
A.1个B.2个
C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com