
【题目】近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产![]() (千部)手机,需另投入成本
(千部)手机,需另投入成本![]() 万元,且
万元,且 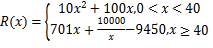 ,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(![]() )求出2020年的利润
)求出2020年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (千部)的函数关系式,(利润=销售额—成本);
(千部)的函数关系式,(利润=销售额—成本);
![]() 2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某高中学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在[50,100]内,发布成绩使用等级制.各等级划分标准见图表.规定:A,B,C三级为合格等级,D为不合格等级.
分数 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
为了解该校高一年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图①所示,样本中原始成绩在80分及以上的所有数据的茎叶图如图②所示.
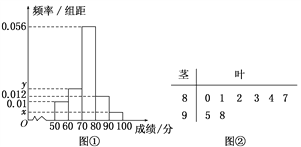
(1)求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
(2)在选取的样本中,从成绩为A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生的成绩是A等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到另一点的距离是在南北方向上行进的距离加上在东西方向上行进的距离,这种距离即“曼哈顿距离”,也叫“出租车距离”.对于平面直角坐标系中的点![]() 和
和![]() ,两点间的“曼哈顿距离”
,两点间的“曼哈顿距离”![]() .
.

(1)如图,若![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 两点坐标分别为
两点坐标分别为![]() 和
和![]() ,求
,求![]() ,
,![]() ,
,![]() ;
;
(2)若点![]() 满足
满足![]() ,试在图中画出点
,试在图中画出点![]() 的轨迹,并求该轨迹所围成图形的面积;
的轨迹,并求该轨迹所围成图形的面积;
(3)已知函数![]() ,试在
,试在![]() 图象上找一点
图象上找一点![]() ,使得
,使得![]() 最小,并求出此时点
最小,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四组函数中,表示同一函数的是
A.f(x)=![]()
![]() ,g(x)=x2–1B.f(x)=
,g(x)=x2–1B.f(x)=![]() ,g(x)=x+1
,g(x)=x+1
C.f(x)=![]() ,g(x)=(
,g(x)=(![]() )2D.f(x)=|x|,g(t)=
)2D.f(x)=|x|,g(t)=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1<x<3},集合B={x|2m<x<1-m}.
(1)当m=-1时,求A∪B;
(2)若AB,求实数m的取值范围;
(3)若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬民族文化,某学校学生全员参与举行了“我爱国学,传诵经典”考试,并从中抽取![]() 名学生的成绩(百分制)作为样本,得到频率分布直方图如图所示.成绩落在
名学生的成绩(百分制)作为样本,得到频率分布直方图如图所示.成绩落在![]() 中的人数为20.
中的人数为20.

(1)求![]() 和
和![]() 的值;
的值;
(2)根据样本估计总体的思想,估计该校学生数学成绩的平均数![]() 和中位数
和中位数![]() ;(同一组数据中的数据以这组数据所在区间中点的值作代表)
;(同一组数据中的数据以这组数据所在区间中点的值作代表)
(3)若成绩在80分以上(含80分)为“国学小达人”.若在样本中,利用分层抽样的方法从“国学小达人”中随机抽取5人,再从中抽取2人赠送一套国学经典,记“抽中的2名学生成绩都不低于90分”为事件![]() ,求
,求![]() ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com