练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆过点，且的离心率为.

    （1）求的方程；

    （2）过的顶点作两条互相垂直的直线与椭圆分别相交于两点.若的角平分线方程为，求的面积及直线的方程.

    【答案】（1）;（2）.

    【解析】试题分析：（1）根据椭圆离心率和椭圆上一点的坐标，列方程组，解方程组可求得椭圆的标准方程.（2）设出过点的直线方程，联立直线的方程和椭圆的方程，求得点的横坐标，由此得到，利用角平分线上的点到两边的距离相等建立方程，可求得斜率，由此求得三角形面积和直线方程.

    试题解析：

    （1）把点代入中，得，又，∴，

    解得，，

    ∴椭圆的方程为.

    （2）设过斜率为的直线为，代入椭圆方程得

    ，①

    则，

    ∴ ，②

    在直线上取一点，则到直线的距离为，

    点到直线的距离为，

    由已知条件，解得或.

    代入②得，，

    ∴的面积 .

    由①得，.

    ∴的方程为，即.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，ABCDA1B1C1D1是正方体，画出图中阴影部分的平面与平面ABCD的交线，并给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体ABCD-A1B1C1D1中，E，F，P，Q，M，N分别是棱AB，AD，DD1，BB1，A1B1，A1D1的中点.求证：

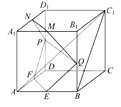
    (1)直线BC1∥平面EFPQ.

    (2)直线AC1⊥平面PQMN.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】.如图，在三棱锥V-ABC中，VO⊥平面ABC，O∈CD，VA=VB，AD=BD，则下列结论中不一定成立的是　(　　)

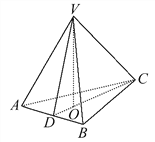
    A. AC=BC

    B. VC⊥VD

    C. AB⊥VC

    D. S△VCD·AB=S△ABC·VO

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆： 过椭圆： ()的短轴端点， ， 分别是圆与椭圆上任意两点，且线段长度的最大值为3．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）过点作圆的一条切线交椭圆于， 两点，求的面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知e为自然对数的底数,设函数,则( )．

    A. 当k=1时,f(x)在x=1处取到极小值 B. 当k=1时,f(x)在x=1处取到极大值

    C. 当k=2时,f(x)在x=1处取到极小值 D. 当k=2时,f(x)在x=1处取到极大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小五、小一、小节、小快、小乐五位同学站成一排，若小一不出现在首位和末位，小五、小节、小乐中有且仅有两人相邻，求能满足条件的不同排法共有多少种？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】16艘轮船的研究中，船的吨位区间为[192，3 246](单位：吨)，船员的人数5～32人，船员人数y关于吨位x的回归方程为=9.5+0.006 2x，

    (1)若两艘船的吨位相差1 000，求船员平均相差的人数.

    (2)估计吨位最大的船和最小的船的船员人数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥，底面是边长为的菱形， ， 为的中点， ，

    与平面所成角的正弦值为.

    (1)在棱上求一点，使平面；

    (2)求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案