
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
分析 根据正切函数的性质结合二倍角公式进行化简求解即可.
解答 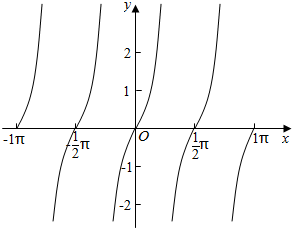 解:y=$\frac{2tanx}{1-tan^2x}$=tan2x,
解:y=$\frac{2tanx}{1-tan^2x}$=tan2x,
由1-tan2x≠0得tan2x≠1,即tanx≠±1,即x≠kπ$±\frac{π}{4}$
即函数的定义域为{x|x≠kπ$±\frac{π}{4}$且x≠kπ+$\frac{π}{2}$},
在每π个单位长度上,函数要去掉一个点($\frac{π}{2}$,0),
函数图象是每两个$\frac{π}{2}$个单位的长度上,重复出现一次相同的图象,则函数的周期是π,
故选:B
点评 本题主要考查三角函数周期的求解,利用三角函数的倍角公式是解决本题的关键.本题要注意定义域,否则容易选错答案,本题容易选答案C.是个易错题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{(x+3)}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{(x+3)}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{(x-3)}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{(x-3)}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二文上月考三数学试卷(解析版) 题型:解答题
如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, ,
,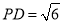 ,
, 为
为 与
与 的交点,
的交点, 为棱
为棱 上一点.
上一点.

(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)若 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com