
【题目】某学生在假期进行某种小商品的推销,他利用所学知识进行了市场调查,发现这种商品当天的市场价格与他的进货量(件)加上20成反比.已知这种商品每件进价为2元.他进100件这种商品时,当天卖完,利润为100元.若每天的商品都能卖完,求这个学生一天的最大利润是多少?获得最大利润时每天的进货量是多少件?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(lnx﹣ax).
(1)a= ![]() 时,求f(x)在点(1,f(1))处的切线方程;
时,求f(x)在点(1,f(1))处的切线方程;
(2)若f(x)存在两个不同的极值x1 , x2 , 求a的取值范围;
(3)在(2)的条件下,求f(x)在(0,a]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣x
(1)求f(x)的解析式;
(2)画出f(x)的图象;
(3)若方程f(x)=k有4个解,求k的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选择意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果整理成条形图如下.

上图中,已知课程![]() 为人文类课程,课程
为人文类课程,课程![]() 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取![]() 的学生作为研究样本组(以下简称“组M”).
的学生作为研究样本组(以下简称“组M”).
(Ⅰ)在“组M”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)为参加某地举办的自然科学营活动,从“组M”所有选择自然科学类课程的同学中随机抽取4名同学前往,其中选择课程F或课程H的同学参加本次活动,费用为每人1500元,选择课程G的同学参加,费用为每人2000元.
(ⅰ)设随机变量![]() 表示选出的4名同学中选择课程
表示选出的4名同学中选择课程![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列;
的分布列;
(ⅱ)设随机变量![]() 表示选出的4名同学参加科学营的费用总和,求随机变量
表示选出的4名同学参加科学营的费用总和,求随机变量![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x≠0).
(x≠0).
(1)证明函数f(x)为奇函数;
(2)判断函数f(x)在[1,+∞)上的单调性,并说明理由;
(3)若x∈[﹣2,﹣3],求函数的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
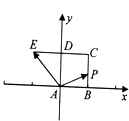
【题目】如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中 ![]() =λ
=λ ![]() +μ
+μ ![]() ,则下列命题正确的是 . (填上所有正确命题的序号)
,则下列命题正确的是 . (填上所有正确命题的序号)
①当点P为AD中点时,λ+μ=1;
②λ+μ的最大值为3;
③若y为给定的正数,则一存在向量 ![]() 和实数x,使
和实数x,使 ![]() =x
=x ![]() +y
+y ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com