
【题目】已知点P到圆(x+2)2+y2=1的切线长与到y轴的距离之比为t(t>0,t≠1);
(1)求动点P的轨迹C的方程;
(2)当![]() 时,将轨迹C的图形沿着x轴向左移动1个单位,得到曲线G,过曲线G上一点Q作两条渐近线的垂线,垂足分别是P1和P2,求
时,将轨迹C的图形沿着x轴向左移动1个单位,得到曲线G,过曲线G上一点Q作两条渐近线的垂线,垂足分别是P1和P2,求![]() 的值;
的值;
(3)设曲线C的两焦点为F1,F2,求t的取值范围,使得曲线C上不存在点Q,使∠F1QF2=θ(0<θ<π).
【答案】(1)(1﹣t2)x2+y2+4x+3=0(2)![]() (3)0<t<
(3)0<t<![]()
【解析】
(1)设P(x,y),则P到圆的切线长为![]() ,利用勾股定理列方程化简即可得出动点P的轨迹C的方程;
,利用勾股定理列方程化简即可得出动点P的轨迹C的方程;
(2)当t![]() 时,轨迹C的方程化为:
时,轨迹C的方程化为: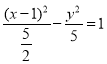 .可得曲线G的方程为
.可得曲线G的方程为 .可得曲线G的渐近线方程为y
.可得曲线G的渐近线方程为y![]() x,y
x,y![]() x.设Q(x0,y0),P1(m,
x.设Q(x0,y0),P1(m,![]() m),P2(n,
m),P2(n,![]() n),
n),![]() ,
,![]() .可得m,n.又y02=2x02﹣5,利用数量积运算性质即可得出;
.可得m,n.又y02=2x02﹣5,利用数量积运算性质即可得出;
(3)对曲线C得类型进行讨论,得出∠F1QF2的最大值,利用三角恒等变换列不等式解出t的范围.
解:(1)圆(x+2)2+y2=1的圆心为M(﹣2,0),半径r=1,
设P(x,y),则P到圆的切线长为![]() ,
,
∴![]() t|x|,
t|x|,
∴(x+2)2+y2﹣1=t2x2,
整理得(1﹣t2)x2+y2+4x+3=0.
则动点P的轨迹C的方程为:(1﹣t2)x2+y2+4x+3=0.
(2)当t![]() 时,轨迹C的方程为﹣2x2+4x+3+y2=0,即
时,轨迹C的方程为﹣2x2+4x+3+y2=0,即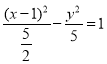 .
.
∴曲线G的方程为 .
.
∴曲线G的渐近线方程为y![]() x,y
x,y![]() x.
x.
设Q(x0,y0),P1(m,![]() m),P2(n,
m),P2(n,![]() n),
n),
∴![]() ,
,![]() .
.
∴m![]() ,n
,n![]() ,
,
∵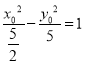 ,∴y02=2x02﹣5,
,∴y02=2x02﹣5,
∴![]() (m﹣x0)(n﹣x0)+(
(m﹣x0)(n﹣x0)+(![]() m﹣y0)(
m﹣y0)(![]() n﹣y0)=(m﹣x0)(n﹣x0)
n﹣y0)=(m﹣x0)(n﹣x0)![]() (x0﹣m)
(x0﹣m)![]() (x0﹣n)
(x0﹣n)
![]() (m﹣x0)(n﹣x0),
(m﹣x0)(n﹣x0),
![]()
![]()
![]() .
.
(3)曲线C的方程可化为(1﹣t2)(x![]() )2+y2
)2+y2![]() 3,
3,
当0<t<1时,曲线C为焦点在x轴上的椭圆,椭圆标准方程为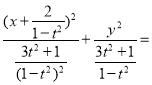 1
1
∴当Q为短轴端点时,∠F1QF2取得最大值,设∠F1QF2的最大值为α,则tan2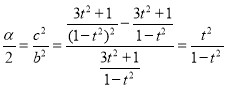 ,
,
∴cosα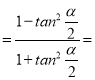 1﹣2t2,
1﹣2t2,
若曲线C上不存在点Q,使∠F1QF2=θ,则θ>α,
∴cosθ<1﹣2t2,解得0<t![]() .
.
当t>1时,曲线C为焦点在x轴的双曲线,∴0<∠F1QF2≤π,
∴当0<θ<π时,曲线C上始终存在的Q使得∠F1QF2=θ.
综上,当0<t![]() 时,曲线C上不存在点Q,使∠F1QF2=θ.
时,曲线C上不存在点Q,使∠F1QF2=θ.


科目:高中数学 来源: 题型:
【题目】如图,D是AC的中点,四边形BDEF是菱形,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() .
.

![]() 若点M是线段BF的中点,证明:
若点M是线段BF的中点,证明:![]() 平面AMC;
平面AMC;
![]() 求平面AEF与平面BCF所成的锐二面角的余弦值.
求平面AEF与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面边长为![]() ,侧棱长为
,侧棱长为![]() 的正四棱柱
的正四棱柱![]() 中,
中,![]() 是侧棱
是侧棱![]() 上的一点,
上的一点,![]() .
.
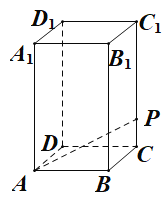
(1)若![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的余弦;
所成角的余弦;
(2)是否存在实数![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式(4kx﹣k2﹣12k﹣9)(2x﹣11)>0,其中k∈R,对于不等式的解集A,记B=A∩Z(其中Z为整数集),若集合B是有限集,则使得集合B中元素个数最少时的实数k的取值范围是__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是_________(请把你认为正确说法的序号都填上).
(1)函数![]() 的最小正周期为
的最小正周期为![]()
(2)若命题![]() :“
:“![]() ,使得
,使得![]() ”,则
”,则![]() :“
:“![]() ,均有
,均有![]() ”
”
(3)![]() 中,
中,![]() 是
是![]() 的充要条件;
的充要条件;
(4)已知点N在![]() 所在平面内,且
所在平面内,且![]() ,则点N是
,则点N是![]() 的重心;
的重心;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用平面截圆柱面,当圆柱的轴与![]() 所成角为锐角时,圆柱面的截面是一个椭圆,著名数学家
所成角为锐角时,圆柱面的截面是一个椭圆,著名数学家![]() 创立的双球实验证明了上述结论.如图所示,将两个大小相同的球嵌入圆柱内,使它们分别位于
创立的双球实验证明了上述结论.如图所示,将两个大小相同的球嵌入圆柱内,使它们分别位于![]() 的上方和下方,并且与圆柱面和
的上方和下方,并且与圆柱面和![]() 均相切.给出下列三个结论:
均相切.给出下列三个结论:
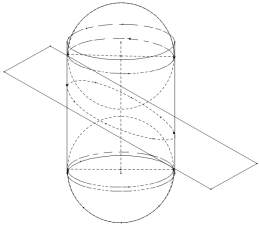
①两个球与![]() 的切点是所得椭圆的两个焦点;
的切点是所得椭圆的两个焦点;
②若球心距![]() ,球的半径为
,球的半径为![]() ,则所得椭圆的焦距为2;
,则所得椭圆的焦距为2;
③当圆柱的轴与![]() 所成的角由小变大时,所得椭圆的离心率也由小变大.
所成的角由小变大时,所得椭圆的离心率也由小变大.
其中,所有正确结论的序号是( )
A.①B.②③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,焦距为
,焦距为![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为弦
为弦![]() 的中点.
的中点.
(1)求椭圆的标准方程;
(2)若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,
,![]() ,若
,若![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com