
| A. | y=${3^{\frac{1}{x+1}}}$ | B. | y=${2^{-\frac{x}{2}}}$ | C. | y=x2+x+1 | D. | y=$\sqrt{1-{2}^{x}}$ |
分析 可看出$\frac{1}{x+1}≠0$,从而${3}^{\frac{1}{x+1}}≠1$,从而判断A错误;显然${2}^{-\frac{x}{2}}>0$,从而判断选析B的函数值域为(0,+∞),这便得出B正确;C中的函数为二次函数,配方便可求其值域;根据指数函数的值域容易得出0≤1-2x<1,从而可求出D中函数的值域.
解答 解:A.$\frac{1}{x+1}≠0$,∴${3}^{\frac{1}{x+1}}≠1$,即该函数的值域不是(0,+∞);
B.$-\frac{x}{2}∈R$,∴${2}^{-\frac{x}{2}}>0$,∴该函数值域为(0,+∞),即该选项正确;
C.$y={x}^{2}+x+1=(x+\frac{1}{2})^{2}+\frac{3}{4}≥\frac{3}{4}$,∴该函数的值域不为(0,+∞);
D.2x>0,1-2x<1;
∴0≤1-2x<1;
∴$0≤\sqrt{1-{2}^{x}}<1$,∴该函数的值域不为(0,+∞).
故选B.
点评 考查函数值域的概念,反比例函数的值域,一次函数的值域,以及指数函数的值域,配方法求二次函数的值域,根据不等式的性质求函数的值域.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
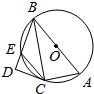 如图,在△ABC中,∠ACB=90°,AB=2AC=8,作△ABC外接圆O的切线CD,作BD⊥CD于D,交圆O于点E,给出下列四个结论:①∠BCD=60°;②DE=2;③BC2=BD•BA;④CE∥AB;则其中正确的序号是①②③④.
如图,在△ABC中,∠ACB=90°,AB=2AC=8,作△ABC外接圆O的切线CD,作BD⊥CD于D,交圆O于点E,给出下列四个结论:①∠BCD=60°;②DE=2;③BC2=BD•BA;④CE∥AB;则其中正确的序号是①②③④.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com