
借助计算器或计算机,用二分法求方程
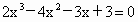 在(0,1)内的近似解(精确到0.01).
在(0,1)内的近似解(精确到0.01).
|
令 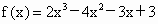 ,∵f(0)=3>0,f(1)=-2<0,说明方程f(x)=0在分别区间(0,1)内有一个零点. ,∵f(0)=3>0,f(1)=-2<0,说明方程f(x)=0在分别区间(0,1)内有一个零点.
取区间 (0,1)的中点 ,用计算器可算得f(0.5)=0.75>0.因为f(0.5)·f(1)<0,所以 ,用计算器可算得f(0.5)=0.75>0.因为f(0.5)·f(1)<0,所以 (0.5,1). (0.5,1).
再取 (0.5,1)的中点 ,用计算器可算得f(0.75)≈-0.66<0.因为f(0.5)·f(0.75)<0,所以 ,用计算器可算得f(0.75)≈-0.66<0.因为f(0.5)·f(0.75)<0,所以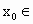 (0.5,0.75). (0.5,0.75).
同理,可得 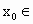 (0.625,0.75), (0.625,0.75),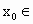 (0.625,0.6825), (0.625,0.6825),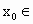 (0.625,0.65375), (0.625,0.65375),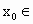 (0.625,0.639375), (0.625,0.639375),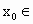 (0.6321875,0.639375), (0.6321875,0.639375),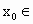 (0.6321875,0.633984375). (0.6321875,0.633984375).
由于 |0.633984375-0.6321875|<0.01,此时区间 (0.6321875,0.633984375)的两个端点精确到0.01的近似值都是0.63,所以方程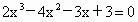 精确到0.01的近似解约为0.63. 精确到0.01的近似解约为0.63.
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com